题目内容
17．
如图，菱形ABCD的周长为32，对角线AC、BD相交于点O，E为BC的中点，则OE=4．
分析 先根据菱形的性质得到BC=8，AC⊥BD，然后根据直角三角形斜边上的中线性质求解．
解答 解：∵四边形ABCD为菱形，
∴BC=8，AC⊥BD，
∵E为BC的中点，
∴OE=$\frac{1}{2}$BC=4．
故答案为4．
点评 本题考查了菱形的性质：有一组邻边相等的平行四边形叫做菱形．熟练掌握菱形的性质（菱形具有平行四边形的一切性质； 菱形的四条边都相等； 菱形的两条对角线互相垂直，并且每一条对角线平分一组对角）．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知：如图，AB∥CD，∠A=∠D，试说明 AC∥DE 成立的理由．
如图，已知?ABCD中，AE平分∠BAD，CF平分∠BCD，分别交BC、AD于E、F．求证：AF=EC．
2．已知一个等腰三角形的一条边长为6，另一条边长为13，则它的周长为（ ）
| A． | 25 | B． | 32 | C． | 25或32 | D． | 19 |
9．
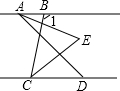如图，己知 AB∥CD，∠BAD 和∠BCD 的平分线交于点E，∠1=100°，∠BAD=m°，则∠AEC的度数为（ ）
如图，己知 AB∥CD，∠BAD 和∠BCD 的平分线交于点E，∠1=100°，∠BAD=m°，则∠AEC的度数为（ ）| A． | m° | B． | （40+$\frac{m}{2}$）° | C． | （40-$\frac{m}{2}$）° | D． | （50+$\frac{m}{2}$）° |
6．
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD，若BD=2，则AB的长是（ ）
如图，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD，若BD=2，则AB的长是（ ）| A． | 2$\sqrt{3}$ | B． | 4 | C． | 4$\sqrt{3}$ | D． | 6 |