题目内容
19. 如图,已知四边形ABCD是矩形,对角线AC,BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E,请探索DC与OE的位置关系,并说明理由.
如图,已知四边形ABCD是矩形,对角线AC,BD交于点O,CE∥BD,DE∥AC,CE与DE交于点E,请探索DC与OE的位置关系,并说明理由.
分析 DC⊥OE,先证明四边形OCED是平行四边形,再由矩形的性质得出OC=OD,证出四边形OCED是菱形,得出对角线互相垂直即可.
解答 解:OE⊥DC,理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴OC=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,AC=BD,
∴OC=OD,
∴四边形OCED是菱形,
∴OE⊥DC.
点评 本题考查了平行四边形的判定、矩形的性质、菱形的判定与性质;熟练掌握矩形的性质和菱形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
9.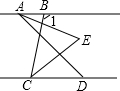 如图,己知 AB∥CD,∠BAD 和∠BCD 的平分线交于点E,∠1=100°,∠BAD=m°,则∠AEC的度数为( )
如图,己知 AB∥CD,∠BAD 和∠BCD 的平分线交于点E,∠1=100°,∠BAD=m°,则∠AEC的度数为( )
 如图,己知 AB∥CD,∠BAD 和∠BCD 的平分线交于点E,∠1=100°,∠BAD=m°,则∠AEC的度数为( )
如图,己知 AB∥CD,∠BAD 和∠BCD 的平分线交于点E,∠1=100°,∠BAD=m°,则∠AEC的度数为( )| A. | m° | B. | (40+$\frac{m}{2}$)° | C. | (40-$\frac{m}{2}$)° | D. | (50+$\frac{m}{2}$)° |
14. 如图,在矩形ABCD中,AB=2BC,在CD上取一点E,使AE=AB,则∠EBC等于( )
如图,在矩形ABCD中,AB=2BC,在CD上取一点E,使AE=AB,则∠EBC等于( )
 如图,在矩形ABCD中,AB=2BC,在CD上取一点E,使AE=AB,则∠EBC等于( )
如图,在矩形ABCD中,AB=2BC,在CD上取一点E,使AE=AB,则∠EBC等于( )| A. | 10° | B. | 15° | C. | 22.5° | D. | 30° |
4.某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长( )
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
9.下列四组线段中,可以构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,4 | C. | 1,2,3 | D. | 4,5,6 |
 甲、乙、丙、丁四人进行飞镖比赛,已知他们每人五次投得的成绩如图所示,那么四人中成绩最稳定的是( )
甲、乙、丙、丁四人进行飞镖比赛,已知他们每人五次投得的成绩如图所示,那么四人中成绩最稳定的是( )