题目内容
16．
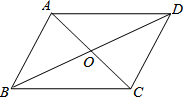如图，平行四边形ABCD的对角线交于点O，且AB=4，△OCD的周长为20，则平行四边形ABCD的两条对角线的和是（ ）| A． | 28 | B． | 32 | C． | 36 | D． | 46 |
分析 由平行四边形的性质和已知条件计算即可，解题注意求平行四边形ABCD的两条对角线的和时要把两条对角线可作一个整体．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD=4，
∵△OCD的周长为20，
∴OD+OC=20-4=16，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=32，
故选B．
点评 本题主要考查了平行四边形的基本性质，并利用性质解题．平行四边形的基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．
练习册系列答案
备战中考寒假系列答案
相关题目
7．
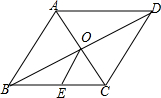如图，在菱形ABCD中，对角线AC与BD相交于点O，E为BC的中点，若BD=2$\sqrt{3}$cm，AC=2cm，则OE的长为（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，E为BC的中点，若BD=2$\sqrt{3}$cm，AC=2cm，则OE的长为（ ）| A． | $\sqrt{3}$cm | B． | 2cm | C． | 1cm | D． | $\frac{\sqrt{3}}{2}$cm |
4．下列图形中∠1与∠2互为对顶角的是（ ）
| A． |  | B． |  | C． |  | D． |  |
1．下列命题中，假命题的是（ ）
| A． | a，b，c是直线，若a∥b，b∥c，则a∥c | |
| B． | a，b，c是直线，若a⊥b，b⊥c，则a∥c | |
| C． | a，b，c是直线，若a⊥b，a⊥b，a⊥c，则b⊥c | |
| D． | a，b，c是直线，若a⊥b，b∥c，则a⊥c |
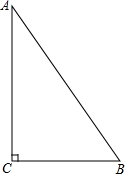（1）如图，试用直尺与圆规在平面内确定一点O，使得点O到Rt△ABC的两边AC、BC的距离相等，并且点O到A、B两点的距离也相等．（不写作法，但需保留作图痕迹）