题目内容
2.已知m2≤$\sqrt{21}$,若$\sqrt{m+2}$是整数,则m=-1或2或-2.分析 先求出|m|<$\sqrt{5}$,根据2<$\sqrt{5}$<3和$\sqrt{m+2}$是整数即可得出答案.
解答 解:∵m2≤$\sqrt{21}$,
∴m2<5,
∴|m|<$\sqrt{5}$,
∵2<$\sqrt{5}$<3,
又∵$\sqrt{m+2}$是整数,
∴m=-1或2或-2,
故答案为:-1,2,-2.
点评 本题考查了估算无理数的大小,能求出|m|$<\sqrt{5}$和估算出$\sqrt{5}$的范围是解此题的关键.

练习册系列答案
相关题目
1.若a2=16,$\root{3}{b}$=-2,则a+b=( )
| A. | -4 | B. | -12 | C. | -4或-12 | D. | ±4或±12 |
11.函数y=(2m-1)x${\;}^{{m}^{2}-2}$是反比例函数,在第一象限内y随x的增大而减小,则m=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | ±$\sqrt{3}$ |
12.下列命题中的真命题是( )
| A. | 两个直角三角形都相似 | |
| B. | 一个直角三角形的两条边和另一个直角三角形的两条边成比例,那么这两个直角三角形相似 | |
| C. | 两个等腰三角形都相似 | |
| D. | 两个等腰直角三角形都相似 |
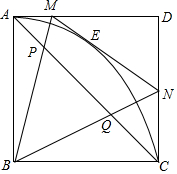 已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.
已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.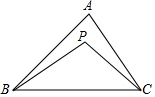 如图,BP与CP相交于点P,∠ABP=$\frac{1}{4}$∠ABC,∠ACP=$\frac{1}{4}$∠ACB,∠A=68°,那么∠P=96°.
如图,BP与CP相交于点P,∠ABP=$\frac{1}{4}$∠ABC,∠ACP=$\frac{1}{4}$∠ACB,∠A=68°,那么∠P=96°.