题目内容
16.A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等.(1)两种机器人每小时分别搬运多少化工原料?
(2)现在两种机器人共同搬运900kg化工原料,搬运3小时候B型机器人因机器维修退出,求B型机器人退出后A型机器人还需搬运多长时间才能搬完?
分析 (1)设B型机器人每小时搬运xkg化工原料,则A型机器人每小时搬运(x+30)kg化工原料,根据时间=工作总量÷工作效率结合A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)根据工作时间=剩余工作量÷工作效率列式计算,此题的及.
解答 解:(1)设B型机器人每小时搬运xkg化工原料,则A型机器人每小时搬运(x+30)kg化工原料,
根据题意得:$\frac{900}{x+30}$=$\frac{600}{x}$,
解得:x=60,
经检验,x=60是分式方程$\frac{900}{x+30}$=$\frac{600}{x}$的解,
∴x+30=90.
答:B型机器人每小时搬运60千克化工原料,A型机器人每小时搬运90千克化工原料.
(2)[900-(60+90)×3]÷90=5(小时).
答:B型机器人退出后A型机器人还需搬运5小时才能搬完.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据时间=工作总量÷工作效率结合A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等列出关于x的分式方程;(2)根据工作时间=剩余工作量÷工作效率列式计算.

练习册系列答案
相关题目
6.下列说法:(1)最大的负整数是-1;(2)数轴上表示数2的点和-2的点到原点距离相等;(3)1.61×104精确到百分位;(4)a+5一定比a大;(5)-23和(-2)3的值相等,正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
请估算口袋中白球的个数约为( )
| 摸球的次数n | 1000 | 1500 | 2000 | 5000 | 8000 | 10000 |
| 摸到白球的次数m | 582 | 960 | 1161 | 2954 | 4842 | 6010 |
| 摸到白球的频率 | 0.582 | 0.64 | 0.5805 | 0.5908 | 0.6053 | 0.601 |
| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
1.若a2=16,$\root{3}{b}$=-2,则a+b=( )
| A. | -4 | B. | -12 | C. | -4或-12 | D. | ±4或±12 |
15.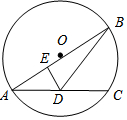 如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
 如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )| A. | 2$\sqrt{15}$ | B. | $\sqrt{35}$ | C. | $\frac{5}{2}$$\sqrt{13}$ | D. | $\frac{7}{2}$$\sqrt{7}$ |
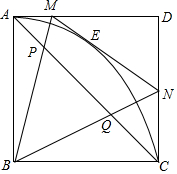 已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.
已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.