题目内容
4．
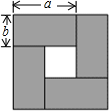如图，是用四张相同的长方形纸片拼成的图形，其中长方形纸片的长为a，宽为b．请利用图中空白部分的面积的不同表示方法写出一个关于a，b的恒等式（a-b）2=（a+b）2-4ab．
分析 空白部分为一个正方形，找到边长，表示出面积；也可用大正方形的面积减去4个矩形的面积表示，然后让这两个面积相等即可．
解答 解：空白部分为正方形，边长为：（a-b），面积为：（a-b）2．
空白部分也可以用大正方形的面积减去4个矩形的面积表示：（a+b）2-4ab．
则（a-b）2=（a+b）2-4ab．
故答案为：（a-b）2=（a+b）2-4ab．
点评 本题考查了完全平方公式的几何意义，用不同的方法表示相应的面积是解题的关键．
练习册系列答案
相关题目
15．
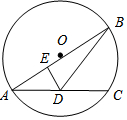如图，AB是⊙O的直径，AC是⊙O的弦，D是AC的中点，过D作DE⊥AB于点E，连结BD．若AD=5，AE=4，则BD的长为（ ）
如图，AB是⊙O的直径，AC是⊙O的弦，D是AC的中点，过D作DE⊥AB于点E，连结BD．若AD=5，AE=4，则BD的长为（ ）| A． | 2$\sqrt{15}$ | B． | $\sqrt{35}$ | C． | $\frac{5}{2}$$\sqrt{13}$ | D． | $\frac{7}{2}$$\sqrt{7}$ |
12．下列命题中的真命题是（ ）
| A． | 两个直角三角形都相似 | |
| B． | 一个直角三角形的两条边和另一个直角三角形的两条边成比例，那么这两个直角三角形相似 | |
| C． | 两个等腰三角形都相似 | |
| D． | 两个等腰直角三角形都相似 |
19．下列各数中，互为相反数的是（ ）
| A． | -2与（-2）2 | B． | -2与2 | C． | -2与-$\frac{1}{2}$ | D． | $\frac{1}{2}$与-2 |
14．若直线y=mx+n经过平面直角坐标系的第一、二、四象限，则点P（m，n）所处的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |