题目内容
19.你能化简(x-1)(x2013+x2012+x2011+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,然后归纳出一些方法.(1)分别化简下列各式:
(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
…
由此猜想:第100个式子(x-1)(x100+x99+…+x+1)=x101-1.
(2)请你利用上面的猜想,化简:
22019+22018+22017+…+2+1.
分析 (1)归纳总结得到规律,写出结果即可;
(2)原式变形后,利用得出的规律计算即可得到结果.
解答 解:(1)(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3+x2+x-x2-x-1=x3-1;
(x-1)(x3+x2+x+1)=x4+x3+x2+x-x3-x2-x-1=x4-1;
第100个式子为(x-1)(x100+x99+…+x+1)=x101-1;
(2)22019+22018+22017+…+2+1
=(2-1)(22019+22018+22017+…+2+1)
=22020-1.
故答案为:(1)x2-1、x3-1、x4-1、(x-1)(x100+x99+…+x+1)=x101-1.
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.计算(2a3)2•a3的结果是( )
| A. | 2a8 | B. | 2a9 | C. | 4a8 | D. | 4a9 |
8.若a3•am=a5÷an,则m与n之间的关系是( )
| A. | m+n=-2 | B. | m+n=2 | C. | mn=$\frac{5}{3}$ | D. | mn=15 |

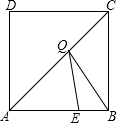 如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为12.
如图,在边长为8的正方形ABCD中,E是AB边上的一点,且AE=6,点Q为对角线AC上的动点,则△BEQ周长的最小值为12.