题目内容

9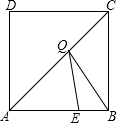．如图，在边长为8的正方形ABCD中，E是AB边上的一点，且AE=6，点Q为对角线AC上的动点，则△BEQ周长的最小值为12．

分析 连接BD，DE，根据正方形的性质可知点B与点D关于直线AC对称，故DE的长即为BQ+QE的最小值，进而可得出结论．

解答 解：连接BD，DE，
∵四边形ABCD是正方形，
∴点B与点D关于直线AC对称，
∴DE的长即为BQ+QE的最小值，
∵AB=8，AE=6，
∴DE=BQ+QE=$\sqrt{A{D}^{2}+A{E}^{2}}$=10，
∵AB=8，AE=6，
∴BE=2，
∴△BEQ周长的最小值=DE+BE=10+2=12．
故答案为：12．

点评 本题考查了正方形的性质、最小值问题、勾股定理、轴对称的性质；熟练掌握正方形的性质，并能进行推理计算是解决问题的关键．

练习册系列答案
相关题目
19．你能化简（x-1）（x2013+x2012+x2011+…+x+1）吗？遇到这样的复杂问题时，我们可以先从简单的情形入手，然后归纳出一些方法．
（1）分别化简下列各式：
（x-1）（x+1）=x2-1；
（x-1）（x2+x+1）=x3-1；
（x-1）（x3+x2+x+1）=x4-1；
…
由此猜想：第100个式子（x-1）（x100+x99+…+x+1）=x101-1．
（2）请你利用上面的猜想，化简：
22019+22018+22017+…+2+1．
20．下列多项式：4a2b（a-b）-6ab2（b-a）中，各项的公因式是（　　）
A．4abB．2abC．ab（a-b）D．2ab（a-b）
17．线段AB与射线AP有一公共端点A．
（1）用直尺和圆规作出以点B为顶点的∠ABQ，使∠ABQ=∠PAB，且BQ和AP相交于点M；
（2）用刻度尺测量MA和MB的长度，你认为MA和MB的大小关系如何？
4．探究问题：
（1）方法感悟：
如图1，在正方形ABCD中，点E、F分别为DC、BC边上的点，且满足∠EAF=45°，连接EF，求证：DE+BF=EF．
感悟解题方法，并完成下列填空：
将△ADE绕点A顺时针旋转90°得到△ABG，此时AD与AB重合，由旋转可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G、B、F在同一条直线上．
∵∠EAF=45°，
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
∵∠1=∠2，∴∠1+∠3=45°．
即∠GAF=∠EAF．
又　AG=AE，AF=AF，∴△GAF≌△EAF．
∴GF=EF，故DE+BF=EF；
（2）方法迁移：
如图2，将Rt△ABC沿斜边翻折得到△ADC，点E、F分别为DC、BC边上的点，且∠EAF=$\frac{1}{2}$∠DAB．试猜想DE、BF、EF之间有何数量关系，并证明你的猜想；
（3）问题拓展：
如图3，在四边形ABCD中，AB=AD，E、F分别为DC、BC上的点，满足∠EAF=$\frac{1}{2}$∠DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．
14．用整式乘法公式计算下列各题：
（1）（2a-b+3）（2a-b-3）
（2）20162-2×2016×2015+20152．
1．计算：
（1）（-a2）•（-2b3）2；
（2）（ab3）2+（-a）2•（b2）3；
（3）${（-2）^2}-{（π-3）^0}+{（\frac{1}{3}）^{-1}}$．
18．已知⊙O的面积2π，则其内接正三角形的面积为$\frac{3\sqrt{3}}{2}$．
19．计算：2sin60°-（-3）2+（-1）2016．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网