题目内容
19.在平面直角坐标系中,抛物线y=ax2-2ax+a+4(a<0)经过点A(-1,0),且与x轴正半轴交于点B,与y轴交于点C,点D是顶点.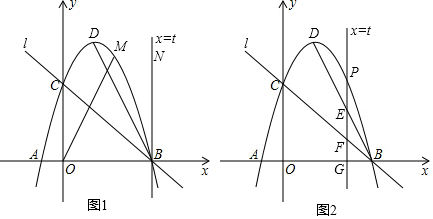
(1)填空:a=-1;顶点D的坐标为(1,4);直线BC的函数表达式为:y=-x+3.
(2)直线x=t与x轴相交于一点.
①当t=3时得到直线BN(如图1),点M是直线BC上方抛物线上的一点.若∠COM=∠DBN,求出此时点M的坐标.
②当1<t<3时(如图2),直线x=t与抛物线、BD、BC及x轴分别相交于点P、E、F、G,试证明线段PE、EF、FG总能组成等腰三角形;如果此等腰三角形底角的余弦值为$\frac{3}{5}$,求此时t的值.
分析 (1)将点A的坐标代入抛物线y=ax2-2ax+a+4中,即可求出a的值;利用顶点坐标公式求出点D的坐标;求出点B、点C的坐标,再利用待定系数法求出解析式即可;
(2)①设点M的坐标为(m,-m2+2m+3),利用tan∠COM=tan∠DBN,列出方程,求出m的值即可求出点M的坐标;
②利用待定系数法求出直线BD的解析式,利用用含t的式子表示出EF、FG、PE的长度,利用三边关系即可证明;底角的余弦值为$\frac{3}{5}$,列出关于t的方程,解得即可.
解答 解:(1)∵抛物线y=ax2-2ax+a+4(a<0)经过点A(-1,0),
∴a+2a+a+4=0,解得:a=-1;
∴抛物线解析式为:y=-x2+2x+3,
∴$-\frac{b}{2a}=-\frac{2}{-2}$=1,$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-1)×3-4}{4×(-1)}$=4,
∴顶点D的坐标为:(1,4);
令x=0,得:y=3,即点C的坐标为(0,3);
∵点A(-1,0),对称轴为直线x=1,
∴1×2-(-1)=3,
∴点B的坐标为(3,0),
设直线BC的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为:y=-x+3;
故答案为:-1,(1,4),y=-x+3;
(2)①设点M的坐标为(m,-m2+2m+3),
∵∠COM=∠DBN,
∴tan∠COM=tan∠DBN,
∴$\frac{m}{-{m}^{2}+2m+3}=\frac{2}{4}$,解得:m=±$\sqrt{3}$,
∵m>0,
∴m=$\sqrt{3}$,
∴点M($\sqrt{3}$,2$\sqrt{3}$);
②设直线BD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{3k+b=0}\\{k+b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴直线BD的解析式为:y=-2x+6;
∴点P(t,-t2+2t+3),点E(t,-2t+6),点F(t,-t+3),
∴PE=(-t2+2t+3)-(-2t+6)=-t2+4t-3,EF=(-2t+6)-(-t+3)=-t+3,FG=-t+3,
∴EF=FG.
∵EF+FG-PE=2(-t+3)-(-t2+4t-3)=(t-3)2>0,
∴EF+FG>PE,
∴当1<t<3时,线段PE,EF,FG总能组成等腰三角形,
由题意的:$\frac{\frac{1}{2}PE}{EF}=\frac{3}{5}$,即$\frac{\frac{1}{2}(-{t}^{2}+4t-3)}{-t+3}=\frac{3}{5}$,
∴5t2-26t+33=0,解得:t=3或$\frac{11}{5}$,
∴1<t<3,
∴t=$\frac{11}{5}$.
点评 本题主要考查二次函数的综合题,解决此题时要灵活运用待定系数法求函数解析式,能用含m或t的式子表示出线段的长度是解决此题的关键.

 特高级教师点拨系列答案
特高级教师点拨系列答案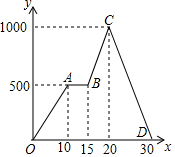 王卉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示,下列结论正确的个数是( )
王卉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示,下列结论正确的个数是( )①整个行进过程花了30分钟;
②整个行进过程共走了1000米;
③前10分钟的速度越来越快;
④在途中停下来休息了5分钟;
⑤返回时速度为100米/分.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 时间t(天) | 1 | 3 | 5 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
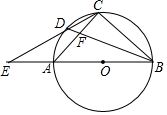 如图,AB是⊙O的直径,点D是$\widehat{AC}$的中点,CD与BA的延长线交于E,BD与AC交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AC}$的中点,CD与BA的延长线交于E,BD与AC交于点F.