题目内容
9.甲仓库有粮120吨,乙仓库有粮90吨.从甲仓库调运多少吨到乙仓库,调剂后甲仓库存粮是乙仓库的一半.分析 通过理解题意可知本题的等量关系为,调剂后:甲仓库的存粮×2=乙仓库存粮,根据这个等量关系,可列出方程,再求解.
解答 解:设从甲仓库调运x吨到乙仓库,可列出方程:(120-x)×2=(90+x),
解得:x=50,
答:从甲仓库调运50吨到乙仓库,调剂后甲仓库的存粮是乙仓库存粮的一半.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$,其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
17.计算${({\sqrt{3}})^2}$的结果是( )
| A. | -3 | B. | 3 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
4.设A=x2+1,B=-2x+x2,则2B-3A可化简为( )
| A. | 4x2+1 | B. | -x2-4x-3 | C. | x2-4x-3 | D. | x2-3 |
1.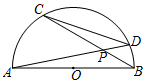 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )| A. | 16:9 | B. | 3:4 | C. | 4:3 | D. | 9:16 |
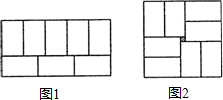 如图所示,两个图案都是由8个大小一样的小长方形拼成的,并且图②中,中央小正方形的面积是1平方厘米.
如图所示,两个图案都是由8个大小一样的小长方形拼成的,并且图②中,中央小正方形的面积是1平方厘米.