题目内容
11.某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:| 时间t(天) | 1 | 3 | 5 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 86 | 76 | 24 | … |
下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的表达式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
分析 (1)从表格可看出每天比前一天少销售2件,所以判断为一次函数关系式;
(2)日利润=日销售量×每件利润,据此分别表示前20天和后20天的日利润,根据函数性质求最大值后比较得结论.
解答 解:(1)经分析知:m与t成一次函数关系.设m=kt+b(k≠0),
将t=1,m=94,t=3,m=90
代入$\left\{\begin{array}{l}{94=k+b}\\{90=3k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=96}\end{array}\right.$,
∴m=-2t+96;
(2)前20天日销售利润为P1元,后20天日销售利润为P2元,
则P1=(-2t+96)($\frac{1}{4}$t+25-20)=-$\frac{1}{2}$(t-14)2+578,
∴当t=14时,P1有最大值,为578元.
P2=(-2t+96)•($\frac{1}{2}$t+40-20)=-t2+8t+1920=(t-44)2-16,
∵当21≤t≤40时,P2随t的增大而减小,
∴t=21时,P2有最大值,为513元.
∵513<578,
∴第14天日销售利润最大,最大利润为578元.
点评 本题考查了二次函数的应用,解题的关键是:(1)熟练掌握各函数的性质和图象特征,针对所给条件作出初步判断后需验证其正确性;(2)最值问题需由函数的性质求解时,正确表达关系式是关键.同时注意自变量的取值范围.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
1.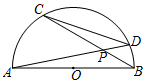 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
 如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )
如图,AB为半圆O的直径,弦AD,BC相交于点P,如果CD=3,AB=4,那么S△PDC:S△PBA等于( )| A. | 16:9 | B. | 3:4 | C. | 4:3 | D. | 9:16 |
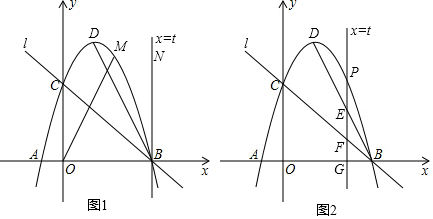

 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20$\sqrt{2}$m,点C与点A在同一水平线上,A、B、P、C在同一平面内.
如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20$\sqrt{2}$m,点C与点A在同一水平线上,A、B、P、C在同一平面内. 如图,若∠1+∠3=180°,则图中与∠1相等的角是∠2,∠6,∠8,与∠1互补的角是∠4,∠5,∠7.
如图,若∠1+∠3=180°,则图中与∠1相等的角是∠2,∠6,∠8,与∠1互补的角是∠4,∠5,∠7.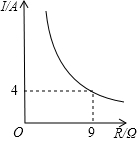 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.