题目内容
8.先化简,再求值.(1)(x+2y)(x-2y)(x2+4y2),其中x=2,y=-1;
(2)[xy(1-x)-2x(y-$\frac{1}{2}$)]•2x3y2+2x4y3(x+1),其中x=-1,y=$\frac{1}{2}$.
分析 (1)首先利用平方差公式计算,进而将已知数据代入求出答案;
(2)直接利用整式乘法运算法则进而化简求出答案.
解答 解:(1)(x+2y)(x-2y)(x2+4y2),
=(x2-4y2)(x2+4y2)
=x4-16y4
将x=2,y=-1代入得:
原式=24-16×(-1)4=16-16=0;
(2)[xy(1-x)-2x(y-$\frac{1}{2}$)]•2x3y2+2x4y3(x+1),
=(xy-x2y-2xy+x)•2x3y2+2x4y3(x+1),
=(-xy-x2y+x)•2x3y2+2x4y3(x+1),
=-2x4y3-2x5y3+2x4y2+2x5y3+2x4y3
=2x4y2,
把x=-1,y=$\frac{1}{2}$代入得:
原式=2×(-1)4×($\frac{1}{2}$)2=$\frac{1}{2}$.
点评 此题主要考查了整式的混合运算,正确掌握整式乘法运算法则是解题关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13.下列说法中正确的个数有( )
①正方体的所有棱长都相等
②圆锥的侧面展开图是扇形
③圆柱的侧面是长方形.
①正方体的所有棱长都相等
②圆锥的侧面展开图是扇形
③圆柱的侧面是长方形.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
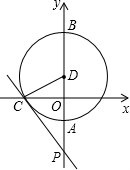 如图⊙D交y轴于A、B两点,交x轴于点C,已知点D的坐标为(0,1),过点C的直线$y=-2\sqrt{2}x-8$与y轴交于点P.
如图⊙D交y轴于A、B两点,交x轴于点C,已知点D的坐标为(0,1),过点C的直线$y=-2\sqrt{2}x-8$与y轴交于点P.