题目内容
17.已知G是△ABC的重心,点D、E分别是AB、AC上的点,DE∥BC,且经过重心G.如果△ABC的周长是30厘米,那么△ADE的周长是20厘米.分析 根据重心的性质得出$\frac{AG}{AF}$=$\frac{2}{3}$,再结合相似三角形的判定与性质得出$\frac{DE}{BC}$=$\frac{AG}{AF}$=$\frac{2}{3}$,进而可得出结论.
解答 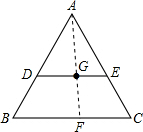 解:连接AG并延长交BC于一点F,
解:连接AG并延长交BC于一点F,
∵点G是△ABC的重心,
∴$\frac{AG}{AF}$=$\frac{2}{3}$,
∵DE∥BC,
∴△ADE∽△ABC,△AGE∽△AFC,△ADG∽△ABF,
∴$\frac{DE}{BC}$=$\frac{AG}{AF}$=$\frac{2}{3}$,
∴$\frac{{C}_{△ADE}}{{C}_{△ABC}}$=$\frac{{C}_{△ADE}}{30}$=$\frac{2}{3}$,解得C△ADE=$\frac{2×30}{3}$=20(厘米).
故答案为:20.
点评 本题考查的是三角形的重心,根据题意画出图形,利用相似三角形的性质求解是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.若代数式2x-y的值是5,则代数式2y-4x+5的值为( )
| A. | -15 | B. | -5 | C. | 5 | D. | 15 |
2.若代数式y2+y-2的值为0,则代数式y3+4y2+y+2014的值为( )
| A. | 2014 | B. | 2015 | C. | 2020 | D. | 2025 |
9.若圆锥的侧面展开图是半圆面,则此圆锥的轴截面是( )
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 顶角为30°的等腰三角形 | D. | 以上都不对 |
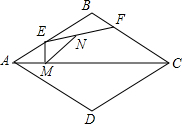 如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.
如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.