题目内容
7.已知方程2x2+bx+a=0(a≠0)的一个根是a.(1)求2a+b的值;
(2)若此方程有两个相等的实数解,求出此方程的解.
分析 (1)根据方程的解的概念将x=a代入方程得a(2a+b+1)=0,由a≠0知2a+b+1=0,可得答案;
(2)由方程有两个相等实数根可得△=0,将b=-2a-1可得关于a的方程,解方程即可得方程的解.
解答 解:(1)∵方程2x2+bx+a=0(a≠0)的一个根是a,
∴2a2+ab+a=0,即a(2a+b+1)=0,
∵a≠0,
∴2a+b+1=0,即2a+b=-1;
(2)∵方程有两个相等实数解,
∴△=b2-8a=0,
由(1)知,2a+b+1=0,即b=-2a-1,
∴(-2a-1)2-8a=0,
整理得:(2a-1)2=0,
解得:a=$\frac{1}{2}$,
故此方程的解为:x=$\frac{1}{2}$.
点评 本题考查了方程的解得概念及一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
17.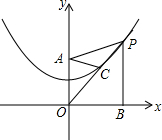 如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
 如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )| A. | PA=PB | B. | ∠POB=45° | C. | PA=2AC | D. | PB=3 |
15.新学期开学初,王刚同学对部分同学暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
(1)王刚同学抽取样本的容量是多少?
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?
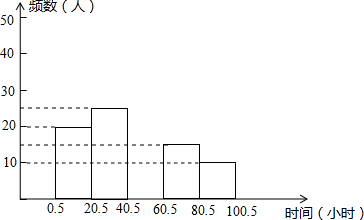
| 时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
| 频 数 | 20 | 25 | 30 | 15 | 10 |
(2)请你根据表中数据补全图中的频数分布直方图;
(3)若该学校有学生1260人,那么大约有多少学生在暑假做家务的时间在40.5~100.5小时之间?

2.统计显示,2015年汕头市中考学生人数和高考学生人数合计大约是13.3万人,将13.3万用科学记数法表示应为( )
| A. | 13.3×102 | B. | 1.33×103 | C. | 1.33×104 | D. | 1.33×105 |
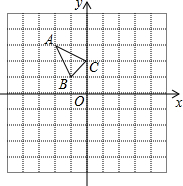 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.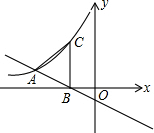 直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.
直线y=-$\frac{1}{2}$x-1与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为-4.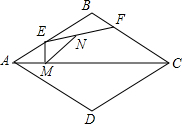 如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.
如图,菱形ABCD的边长为8,∠BAD=60°,点E在AB上运动,点F在BC上运动(E,F两点可以和菱形的顶点重合),且EF=4,点N是线段EF的中点,ME⊥AC垂足为M,则MN的最小值是2$\sqrt{3}$.