题目内容
18.化简求值:$\frac{1}{\sqrt{2}+\sqrt{4}}$+$\frac{1}{\sqrt{4}+\sqrt{6}}$+…+$\frac{1}{\sqrt{48}+\sqrt{50}}$.分析 根据平方差公式,可分母有理化,根据实数的运算,可得答案.
解答 解:原式=$\frac{1}{2}$($\sqrt{4}$-$\sqrt{2}$+$\sqrt{6}$-$\sqrt{4}$+…+$\sqrt{50}$-$\sqrt{48}$)=$\frac{1}{2}$($\sqrt{50}$-$\sqrt{2}$)=2.
点评 本题考查了分母有理化,利用分母有理化得出互为相反数的项是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若圆锥的侧面展开图是半圆面,则此圆锥的轴截面是( )
| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 顶角为30°的等腰三角形 | D. | 以上都不对 |
10.在日历上,我们发现某些数会满足一定的規律,比如2016年1月份的日历,我们设计这样的算法:任意选择其中的2×2方框,将方框中4个位置上的数先平方,然后交叉求和,再相减 请你按照这个算法完成下列计算,并回答以下问题
[2016年1月份的日历]
(1)计算:(12+92)-(22+82)=14,(102+182)-(112+172)=14,自己任选一个有4个数的方框进行计算14
(2)通过计算你发现什么规律,并说明理由.
[2016年1月份的日历]
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
(2)通过计算你发现什么规律,并说明理由.
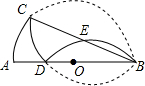 如图,AB是半圆O的直径,将半圆沿弦BC折叠,折叠后的圆弧与AB交于点D,再将弧BD沿AB对折后交弦BC于E,若E恰好是BC的中点,则BC:AB=$\frac{\sqrt{14}}{4}$.
如图,AB是半圆O的直径,将半圆沿弦BC折叠,折叠后的圆弧与AB交于点D,再将弧BD沿AB对折后交弦BC于E,若E恰好是BC的中点,则BC:AB=$\frac{\sqrt{14}}{4}$.