题目内容
9.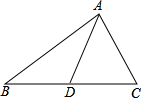 如图,△ABC中,点D在BC上,连结AD.
如图,△ABC中,点D在BC上,连结AD.(1)请你添加一个条件,使得△DCA与△ACB相似;
(2)在(1)的条件下,求证:$\frac{A{D}^{2}}{A{B}^{2}}$=$\frac{DC}{BC}$.
(要求:用两种方法加以证明)
分析 (1)利用两角对应相等的两三角形相似即可;
(2)方法一:利用相似三角形得出的比例式代换即可得出面积;
方法二:利用同高的两三角形面积的比等于底的比和相似三角形的面积比是相似比的平方这一性质即可.
解答 解:(1)添加的条件为∠B=∠CAD,
理由:∵∠B=∠CAD,∠C=∠C
∴△DCA∽△ACB,
(2)方法一:由(1)知,△DCA∽△ACB,
∴$\frac{AD}{AB}=\frac{CD}{AC}=\frac{AC}{BC}$,
∴$\frac{A{D}^{2}}{A{B}^{2}}$=$\frac{AD}{AB}×\frac{AD}{AB}$=$\frac{CD}{AC}×\frac{AC}{BC}$=$\frac{CD}{BC}$,
方法二:如图,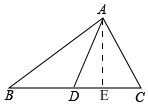
过点A作AE⊥BC,
由(1)知,△DCA∽△ACB,
∴$\frac{{S}_{△ACD}}{{S}_{△BCA}}=(\frac{AD}{AB})^{2}=\frac{A{D}^{2}}{A{B}^{2}}$,
∵S△ACD=$\frac{1}{2}$CD×AE,
S△BCA=$\frac{1}{2}$BC×AE,
∴$\frac{{S}_{△ACD}}{{S}_{△BCA}}=\frac{\frac{1}{2}CD×AE}{\frac{1}{2}BC×AE}=\frac{CD}{BC}$,
∴$\frac{A{D}^{2}}{A{B}^{2}}$=$\frac{DC}{BC}$.
点评 此题是相似三角形的性质和判定,主要考查了三角形的面积的计算方法,同高的两三角形的面积比等于底的比,解本题的关键是添加出条件.

练习册系列答案
相关题目
5.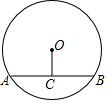 排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
 排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )
排水管的截面如图,水面宽AB=8,圆心O到水面的距离OC=3,则排水管的半径等于( )| A. | 5 | B. | 6 | C. | 8 | D. | 4 |