题目内容
7.求3|x-1|+2|x-2|的最小值2,此时x=1.分析 利用x的取值不同分别得出最小值,进而得出答案
解答 解:当x<1时,则3|x-1|+2|x-2|=3(1-x)+2(2-x)=7-5x>2,则没有最小值;
当1≤x<2时,则3|x-1|+2|x-2|=3(x-1)+2(2-x)=x+1,易得2≤x+1<3,则最小值为2;
当x≥2时,则3|x-1|+2|x-2|=3(x-1)+2(x-2)=5x-7,易得5x-7≥3,则最小值为3;
综上所述3|x-1|+2|x-2|的最小值为2,此时x=1.
故答案为:2,1.
点评 此题主要考查了绝对值函数最值求法,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
19. 如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )
如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )
 如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )
如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 以上都不是 |
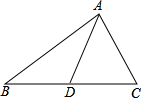 如图,△ABC中,点D在BC上,连结AD.
如图,△ABC中,点D在BC上,连结AD.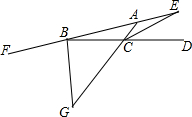 如图所示,在△ABC中,点D是BC延长线上的点,点F是AB延长线上的点.∠ACD的平分线交BA延长线于点E,∠FBC的平分线交AC延长线于点G.若CE=BC=BG,则∠ABC的度数12度.
如图所示,在△ABC中,点D是BC延长线上的点,点F是AB延长线上的点.∠ACD的平分线交BA延长线于点E,∠FBC的平分线交AC延长线于点G.若CE=BC=BG,则∠ABC的度数12度. 如图,在△ABC中,∠C=100°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,求∠APD的度数.
如图,在△ABC中,∠C=100°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,求∠APD的度数.