题目内容
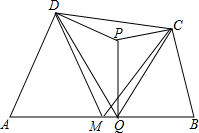 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.考点:四点共圆,全等三角形的判定与性质,直角三角形斜边上的中线,三角形中位线定理,平行四边形的判定与性质,圆周角定理
专题:证明题
分析:连接AP、BP,取AP的中点E,取BP的中点F,连接DE、ME、QE、CF、QF、MF,根据“三角形中位线定理”及“直角三角形斜边上的中线等于斜边的一半”可证得四边形PEMF是平行四边形、△DEM≌△MFC,即可得到∠PEM=∠PFM,∠DEM=∠MFC,则有∠DEP=∠CFP,由此可得到∠DAP=∠PBC.易证D、A、Q、P四点共圆,根据圆周角定理可得∠PQD=∠DAP.同理可得∠PQC=∠PBC,即可得到∠PQC=∠PQD.
解答:证明:连接AP、BP,取AP的中点E,取BP的中点F,连接DE、ME、QE、CF、QF、MF,如图.
∵E为AP的中点,F为BP的中点,M为AB的中点,
∴EM∥BP,EM=
BP,MF∥AP,MF=
AP.
∵E为AP的中点,F为BP的中点,∠ADP=∠BCP=90°,
∴DE=AE=EP=
AP,FC=PF=BF=
BP,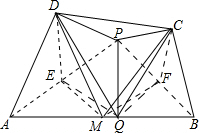
∴DE=MF,EM=FC.
在△DEM和△MFC中,
,
∴△DEM≌△MFC(SSS),
∴∠DEM=∠MFC.
∵EM∥BP,MF∥AP,
∴四边形PEMF是平行四边形,
∴∠PEM=∠PFM.
又∵∠DEM=∠MFC,
∴∠DEP=∠CFP.
∵DE=AE,FC=BF,
∴∠DAE=∠ADE=
∠DEP,∠FBC=∠FCB=
∠CFP,
∴∠DAE=∠FBC,即∠DAP=∠PBC.
∵∠ADP=∠AQP=90°,E为AP中点,
∴ED=EA=EQ=EP=
AP,
∴D、A、Q、P四点共圆,
∴∠PQD=∠DAP.
同理可得:∠PQC=∠PBC,
∴∠PQD=∠PQC.
∵E为AP的中点,F为BP的中点,M为AB的中点,
∴EM∥BP,EM=
| 1 |
| 2 |
| 1 |
| 2 |
∵E为AP的中点,F为BP的中点,∠ADP=∠BCP=90°,
∴DE=AE=EP=
| 1 |
| 2 |
| 1 |
| 2 |

∴DE=MF,EM=FC.
在△DEM和△MFC中,
|
∴△DEM≌△MFC(SSS),
∴∠DEM=∠MFC.
∵EM∥BP,MF∥AP,
∴四边形PEMF是平行四边形,
∴∠PEM=∠PFM.
又∵∠DEM=∠MFC,
∴∠DEP=∠CFP.
∵DE=AE,FC=BF,
∴∠DAE=∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAE=∠FBC,即∠DAP=∠PBC.
∵∠ADP=∠AQP=90°,E为AP中点,
∴ED=EA=EQ=EP=
| 1 |
| 2 |
∴D、A、Q、P四点共圆,
∴∠PQD=∠DAP.
同理可得:∠PQC=∠PBC,
∴∠PQD=∠PQC.
点评:本题主要考查了三角形中位线定理、直角三角形斜边上的中线等于斜边的一半、平行四边形的判定与性质、全等三角形的判定与性质、四点共圆的判定、圆周角定理、等腰三角形的性质等知识,综合性强,难度比较大,由线段的中点联想到三角形中位线定理是解决本题的关键.

练习册系列答案
相关题目
 实数a,b在数轴上的位置如图所示,则式子
实数a,b在数轴上的位置如图所示,则式子| a2 |
| b2 |
| A、a+b | B、a-b |
| C、-a-b | D、-a+b |
 如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=a,CE=b.则两条凳子的高度之和为
如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=a,CE=b.则两条凳子的高度之和为 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求(
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求(

 观察函数y=
观察函数y= 如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC=
如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC= 如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.