题目内容

如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，求（
CD
AC
）2+（
CD
BC
）2．
考点：勾股定理
专题：
分析：相似三角形的判定AA得出△ACB∽△ADC∽△CDB，得出
CD
AC
=
BD
BC
，再把要求的式子进行转换即可得出答案．
解答：解：∵在Rt△ABC中，∠ACB=90°，CD⊥AB，
∴△ACB∽△ADC∽△CDB，
∴
CD
AC
=
BD
BC
，即
CD2
AC2
=
BD2
BC2
，
∵BD2+CD2=BC2，
∴
CD2
AC2
+
CD2
BC2
=
BD2
BC2
+
CD2
BC2
=
BC2
BC2
=1，
∴（
CD
AC
）2+（
CD
BC
）2=1．
点评：此题考查了勾股定理，根据相似三角形的判定得出△ACB∽△ADC∽△CDB是本题的关键．
练习册系列答案
相关题目
已知2xm+1y4与-x4y2n是同类项，mn=
 
．
如果你是“神州八号”的总设计师，发射之前需要检测零部件的安装是否到位，需采用哪种调查方式
 
．
如图，OM平分∠AOB，ON平分∠BOC，∠AOC=120°，则∠MON=
 
．
如图①，在Rt△ABC中，∠BAC=90°，AB=AC，E是AC上一点，且AE=nEC，AF⊥BE于G，交BC于F．
（1）作AD⊥BC于D，交BE于H，求证：△ABH≌△CAF．
（2）连接EF，当n=
 
时，∠AEB=∠CEF（直接写出结论，不必证明）
（3）如图②，M是EC的中点，连接MF，当∠AEB=∠CMF时，求n的值．
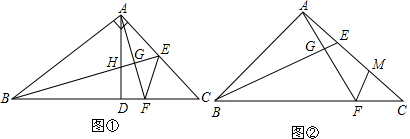
如图，在矩形ABCD中，AB=9，BC=12，点E是BC的中点，点F是CD边上的任意一点，当△AEF的周长最小时，DF=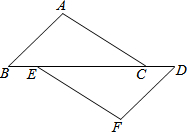
 
．
如图，已知点B，E，C，D在同一直线上，AB=FD，∠B=∠D，请你添加一个条件，使AC=FE，并给出证明（不再添加其它线段，不再标注或使用其他字母）．你添加的条件是：
 
．
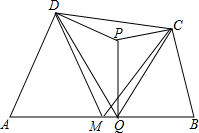如图，在凸四边形ABCD中，M为边AB的中点，且MC=MD，分别过点C、D作边BC、AD的垂线，设两条垂线的交点为P，过点P作PQ⊥AB于Q，求证：∠PQC=∠PQD．
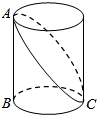如图，已知圆柱底面的周长为2m，圆柱高为1m，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网