题目内容
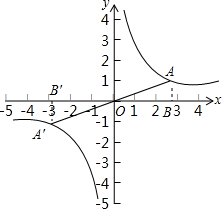 观察函数y=
观察函数y=| 4 |
| x |
(1)写出图中A,A′两点的坐标:A(2
| 2 |
| 2 |
(2)如果分别过点A和A′作x轴的垂线,垂足分别是B和B′,那么下列的判断中,正确的有
①OA=OA′;②∠AOB=∠A′OB′;③点A,O,A′在同一条直线上;④S△AOB=4.
(3)当x=-2时,y=
考点:反比例函数综合题
专题:数形结合
分析:(1)根据反比例函数图象上点的坐标特征,分别计算自变量为2
和-2
的函数值即可;
(2)根据点A与点A′的坐标特征得到点A与点B关于原点对称,则OA=OA′,OB=OB′,于是可证明Rt△AOB≌Rt△A′OB′,所以∠AOB=∠A′OB′,点A,O,A′在同一条直线上;如果根据三角形面积公式可计算出S△AOB=2,这样可对4个结论进行判断;
(3)根据反比例函数图象上点的坐标特征,分别计算自变量为-2的函数值和函数值为-1所对应的自变量的值,然后根据反比例函数的性质求解.
| 2 |
| 2 |
(2)根据点A与点A′的坐标特征得到点A与点B关于原点对称,则OA=OA′,OB=OB′,于是可证明Rt△AOB≌Rt△A′OB′,所以∠AOB=∠A′OB′,点A,O,A′在同一条直线上;如果根据三角形面积公式可计算出S△AOB=2,这样可对4个结论进行判断;
(3)根据反比例函数图象上点的坐标特征,分别计算自变量为-2的函数值和函数值为-1所对应的自变量的值,然后根据反比例函数的性质求解.
解答:解:(1)当x=2
时,y=
=
=
,则A(2
,
);
当x=-2
时,y=
=-
=-
,则A′(-2
,-
);
(2)∵A(2
,
),A′(-2
,-
),
∴点A与点B关于原点对称,
∴OA=OA′,OB=OB′,
∴Rt△AOB≌Rt△A′OB′,
∴∠AOB=∠A′OB′,点A,O,A′在同一条直线上;所以①②③正确;
S△AOB=
×2
×
=2,所以④错误;
(3)当x=-2时,y=
=
=-2;
当x<-2时,y的取值范围是y>-2;
当y=-1时,
=-1,解得x=-4,所以当x≤-4或x>0时,y≥-1.
故答案为
,-
;①②③;-2,x≤-4或x>0.
| 2 |
| 4 |
| x |
| 4 | ||
2
|
| 2 |
| 2 |
| 2 |
当x=-2
| 2 |
| 4 |
| x |
| 4 | ||
2
|
| 2 |
| 2 |
| 2 |
(2)∵A(2
| 2 |
| 2 |
| 2 |
| 2 |
∴点A与点B关于原点对称,
∴OA=OA′,OB=OB′,
∴Rt△AOB≌Rt△A′OB′,
∴∠AOB=∠A′OB′,点A,O,A′在同一条直线上;所以①②③正确;
S△AOB=
| 1 |
| 2 |
| 2 |
| 2 |
(3)当x=-2时,y=
| 4 |
| x |
| 4 |
| -2 |
当x<-2时,y的取值范围是y>-2;
当y=-1时,
| 4 |
| x |
故答案为
| 2 |
| 2 |
点评:本题考查了反比例函数的综合题:熟练掌握反比例函数的性质和反比例函数图象上点的坐标特征.利用图象解决问题,从图上获取有用的信息,是解题的关键所在.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
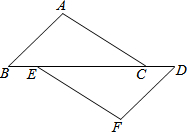 如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是:
如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是: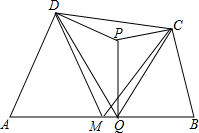 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.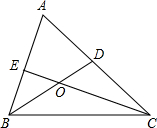 如图,△ABC的两条角平分线BD,CE交于点O
如图,△ABC的两条角平分线BD,CE交于点O 由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是
由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是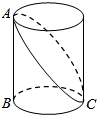 如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为