题目内容
 如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=a,CE=b.则两条凳子的高度之和为
如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知DC=a,CE=b.则两条凳子的高度之和为考点:全等三角形的应用
专题:
分析:利用等腰三角形的性质结合全等三角形的判定方法得出即可.
解答:解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
故DC=BE=a,AD=CE=b,
则两条凳子的高度之和为:a+b.
故答案为:a+b.
则∠DAC=∠BCE,
在△ACD和△CBE中,
|
∴△ACD≌△CBE(AAS),
故DC=BE=a,AD=CE=b,
则两条凳子的高度之和为:a+b.
故答案为:a+b.
点评:此题主要考查了全等三角形的判定与性质,得出△ACD≌△CBE是解题关键.

练习册系列答案
相关题目
 如图所示,下列判断正确的是( )
如图所示,下列判断正确的是( )| A、若∠1=∠2,则AD∥BC |
| B、若∠1=∠2,则AB∥CD |
| C、若∠A=∠3,则AD∥BC |
| D、若∠3+∠ADC=180°,则AB∥CD |
 如图,数轴上表示1、
如图,数轴上表示1、 如图,OM平分∠AOB,ON平分∠BOC,∠AOC=120°,则∠MON=
如图,OM平分∠AOB,ON平分∠BOC,∠AOC=120°,则∠MON=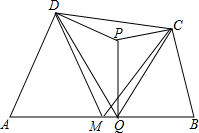 如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.
如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD,分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P,过点P作PQ⊥AB于Q,求证:∠PQC=∠PQD.