题目内容
4. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且AD⊥AB,求证:BC=AB+CD.
分析 在BC上取点F,使BF=BA,连接PF,由角平分线的性质可以得出∠ABP=∠FBP,从而可以得出△ABP≌△FBP,可以得出∠A=∠BFP,进而可以得出△CDP≌△CFP,就可以得出CD=CF,即可得出结论.
解答 解:在BC上取点F,使BF=BA,连接PF,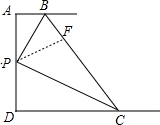
∵BP、CP分别是∠ABC和∠BCD的平分线,
∴∠ABP=∠FBP,∠DCP=∠FCP.
在△ABP和△FBP中,
$\left\{\begin{array}{l}{AB=FB}\\{∠ABP=∠FBP}\\{BP=BP}\end{array}\right.$
∴△ABP≌△FBP(SAS),
∴∠A=∠BFP.
∵AB∥CD,
∴∠A+∠D=180°,
∴∠BFP+∠D=180.
∵∠BFP+∠CFP=180°,
∴∠CFP=∠D.
在△CDE和△CFE中,
$\left\{\begin{array}{l}{∠CFP=∠D}\\{∠FCP=∠DCP}\\{CP=CP}\end{array}\right.$,
∴△CDP≌△CFP(AAS),
∴CF=CD.
∵BC=BF+CF,
∴BC=AB+CD.
点评 本题考查了角平分线的性质的运用,全等三角形的判定及性质的运用,解答时运用截取法正确作辅助线是关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
9.已知点G是等边△ABC的重心,AB=6,P为AB边上的一个动点,则P、G两点间距离的最小值是( )
| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
 如图,长方形ABCD的对角线AC与BD相交于点O,以O为原点建立直角坐标系,使x轴和y轴分别与长方形两邻边平行.已知AD=9,AB=4,求:
如图,长方形ABCD的对角线AC与BD相交于点O,以O为原点建立直角坐标系,使x轴和y轴分别与长方形两邻边平行.已知AD=9,AB=4,求: 如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.
如图,△ABC内接⊙O中,AB=AC=5cm,BC=6cm,求⊙O的半径.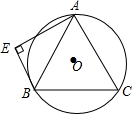 如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.
如图,等边△ABC内接于⊙O,BE与⊙O相切于点B,AE⊥BE,⊙O的半径为10,求AE的长.