题目内容
15．解方程组（1）$\left\{\begin{array}{l}{3x-y=5}\\{5x+2y=15}\end{array}\right.$
（2）$\left\{\begin{array}{l}{\frac{2（x-y）}{3}-\frac{x+y}{4}=-1}\\{6（x+y）-4（2x-y）=16}\end{array}\right.$．
分析 （1）根据代入消元法，可得方程组的解；
（2）根据代入消元法，可得方程组的解．
解答 解：（1）由 ①，得
y=3x-5．③
把③代入②，得
5x+2（3x-5）=15．
解这个方程，得
x=$\frac{25}{11}$．
把x=$\frac{25}{11}$代入③，得
y=$\frac{20}{11}$．
所以原方程的解为$\left\{\begin{array}{l}{x=\frac{25}{11}}\\{y=\frac{20}{11}}\end{array}\right.$．
（2）原方程组整理得：$\left\{\begin{array}{l}{5x-11y=-12①}\\{x-5y=-8②}\end{array}\right.$．
由②，得
x=5y-8，③
把③代入①，得
5（5y-8）-11y=-12．
解这个方程，得
y=2．
把y=2代入③，得
x=2．
这个方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$．
点评 本题考查了解二元一次方程组，先化简方程组，再利用代入消元法解方程组．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．一个角的补角是它的余角的度数的3倍，则这个角的度数是（ ）
| A． | 45° | B． | 50° | C． | 55° | D． | 60° |
3．
某中学计划成立多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校部分学生选择社团的意向，并将调查结果绘制成如下统计表（不完整）：
某校被调查学生选择社团意向统计表
根据统计图表中的信息，解答下列问题：
（1）请直接写出本次调查的总人数以及a和b的值；
（2）将条形统计图补充完整．
某中学计划成立多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校部分学生选择社团的意向，并将调查结果绘制成如下统计表（不完整）：某校被调查学生选择社团意向统计表
| 选择意向 | 文学欣赏 | 科学实验 | 音乐艺术 | 手工制作 | 体育运动 | 其他 |
| 所占百分比 | a | 22.5% | b | 10% | 20% | 2.5% |
（1）请直接写出本次调查的总人数以及a和b的值；
（2）将条形统计图补充完整．
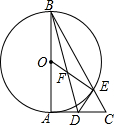如图，△ABC中．△BAC=90°，以AB为直径作⊙O交BC于E，D为AC的中点，连结DE．
一次函数y=kx+b（k，b是常数，k≠0）图象如图所示，则不等式kx+b＞0的解集是x＞-2．