题目内容
9.已知直线y=-$\frac{1}{3}$x+1与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰直角三角形ABC,∠BAC=90度,在x轴上存在一点Q,使得△QAB的面积等于△ABC的面积,则Q点的坐标为(13,0)或(-7,0).分析 由直线y=-$\frac{1}{3}$x+1与x轴、y轴交于A、B两点,即可求得点A与B的坐标,又由等腰直角△ABC,且∠BAC=90°,即可求得AB与AC的值,则可求得△ABC的面积,继而求得答案.
解答 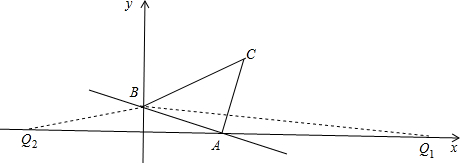 解:∵直线y=-$\frac{1}{3}$x+1与x轴、y轴交于A、B两点,
解:∵直线y=-$\frac{1}{3}$x+1与x轴、y轴交于A、B两点,
∴点A的坐标为:(3,0),点B的坐标为:(0,1),
∴OA=3,OB=1,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{10}$,
∵等腰直角△ABC,∠BAC=90°,
∴AC=AB=$\sqrt{10}$,
∴S△ABC=$\frac{1}{2}$×AB×AC=$\frac{1}{2}$×$\sqrt{10}$×$\sqrt{10}$=5,
∵S△QAB=S△ABC,
∴S△QAB=$\frac{1}{2}$AQ•OB=$\frac{1}{2}$×AQ×1=5,
∴AQ=10,
∴点Q的坐标为(13,0)或(-7,0).
故答案为:(13,0)或(-7,0).
点评 此题考查了点与一次函数的关系、等腰直角三角形的性质以及三角形面积的求解方法等知识.此题难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
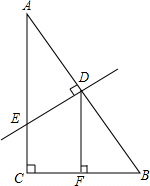 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB、AC于点D、E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线分别交AB、AC于点D、E.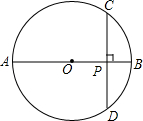 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.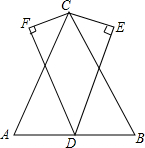 如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.
如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.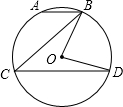 如图,在⊙O中,弦AB∥弦CD,若∠OBD=50°,求∠ABC的度数.
如图,在⊙O中,弦AB∥弦CD,若∠OBD=50°,求∠ABC的度数. 如图所示,∠BAC=85°,BF平分∠ABC交AC于点F,∠BFC=100°,求∠C的度数.
如图所示,∠BAC=85°,BF平分∠ABC交AC于点F,∠BFC=100°,求∠C的度数.