题目内容
14.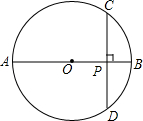 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
分析 连接OC,先由垂径定理求得CP=4,然后再在Rt△OCP中,利用勾股定理列方程求解即可.
解答 解:连接OC.
∵AB是⊙O的直径,弦CD⊥AB,
∴CP=PD=4.
∵OC=OB=r.
∴OP+OP-1=r.
∴OP=$\frac{r+1}{2}$.
在Rt△OPC中,由勾股定理得:OC2=PC2+OP2,即${r}^{2}={4}^{2}+(\frac{r+1}{2})^{2}$.
解得:r=5(负根以舍去).
所以圆的半径为5.
点评 本题主要考查的是垂径定理、勾股定理,利用勾股定理列出关于r的方程是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
19.
| 多项式 | 多项式的项数 | 各项的系数 | 多项式的次数 |
| -2x+1 | 2 | -2,1 | 1 |
| x2-5x4+3 | 3 | 1,-5,3 | 4 |
| x2y+xy | 2 | 1,1 | 3 |
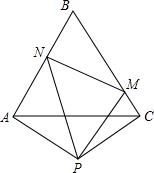 如图,等边△ABC的边长为2,且PA=PC,∠APC=120°,现有∠MPN=60°,将∠MPN绕着P点旋转,使其两边分别与AB、BC交于点N、M.试判断在旋转过程中,△BMN的周长是否发生变化?若不变,请求出周长;若变化,请说明理由.
如图,等边△ABC的边长为2,且PA=PC,∠APC=120°,现有∠MPN=60°,将∠MPN绕着P点旋转,使其两边分别与AB、BC交于点N、M.试判断在旋转过程中,△BMN的周长是否发生变化?若不变,请求出周长;若变化,请说明理由. 如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是$\sqrt{74}$.
如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是$\sqrt{74}$.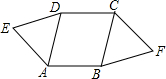 如图,△ADE和△BCF是ABCD外的两个等边三角形,用旋转的知识说明△ADE和△BCF成中心对称.
如图,△ADE和△BCF是ABCD外的两个等边三角形,用旋转的知识说明△ADE和△BCF成中心对称.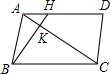 如图,H为平行四边形ABCD中AD边上一点,且AH=$\frac{1}{2}$DH,AC和BH交于点K,求$\frac{AK}{KC}$的值.
如图,H为平行四边形ABCD中AD边上一点,且AH=$\frac{1}{2}$DH,AC和BH交于点K,求$\frac{AK}{KC}$的值.