题目内容
1.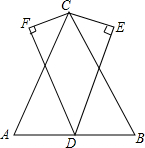 如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.
如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.
分析 连接CD,证得△ECD≌△FCD,得出∠CDF=∠CDE,利用等腰三角形的“三线合一”得出∠CDA=∠CDB=90°,进一步求得结论即可.
解答 证明:如图,
连接CD,
在Rt△ECD和Rt△FCD中,
$\left\{\begin{array}{l}{CF=CE}\\{CD=CD}\end{array}\right.$,
∴Rt△ECD≌Rt△FCD,
∴∠CDF=∠CDE,
∵CA=CB,D是AB的中点,
∴CD⊥AB,
∴∠CDA=∠CDB=90°,
∴∠ADF=∠BDE.
点评 此题考查三角形全等的判定与性质,等腰三角形的性质,掌握三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
11.一元二次方程2x2+6x=9的二次项系数、一次项系数、常数项分别是( )
| A. | 2,6,9 | B. | 6,2,9 | C. | 2,6,-9 | D. | 6,2,-9 |
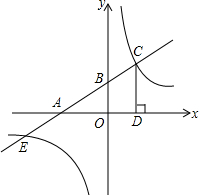 已知直线l1:y1=$\frac{1}{2}$x+2分别交x轴,y轴于点A、B,点C是该直线上在第一象限内的一点,作CD⊥x轴于点D,使得S△ACD=9,再过点C作一条双曲线y2=$\frac{k}{x}$
已知直线l1:y1=$\frac{1}{2}$x+2分别交x轴,y轴于点A、B,点C是该直线上在第一象限内的一点,作CD⊥x轴于点D,使得S△ACD=9,再过点C作一条双曲线y2=$\frac{k}{x}$ 如图,在直线CD上有一动点P,P在CD上从右往左运动的过程中,找出:
如图,在直线CD上有一动点P,P在CD上从右往左运动的过程中,找出: