题目内容
8．设从南安到福州乘坐汽车所需的时间是t（小时），汽车的平均速度为v（千米/时），则下面刻画v与t的函数关系的图象是（ ）| A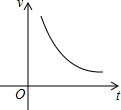． |  | B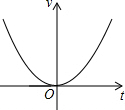． |  | C． |  | D． |  |
分析 因为从南安到福州的路程不变，根据v=$\frac{s}{t}$（t＞0），可知v与t函数关系的图象是反比例函数，
解答 解：根据题意可知v=$\frac{s}{t}$（t＞0，s是常数）．
故选：A．
点评 考查了函数的图象，现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
4．下列不能用平方差公式计算的是（ ）
| A． | （2a+1）（2a-1） | B． | （2a-1）（-2a-1） | C． | （a+b）（-a-b） | D． | （a+b）（b-a） |
5．已知代数式$\sqrt{1-x}$+$\sqrt{\frac{1}{x}}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≥1 | B． | 0＜x≤1 | C． | x＞0 | D． | 0≤x≤1 |
16．已知$a=\frac{\sqrt{3}-1}{2}$，则$\frac{2{a}^{3}+6{a}^{2}+a}{2{a}^{2}-1}$=（ ）
| A． | -$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $-\sqrt{3}+2$ | D． | $\sqrt{3}$+2 |
13．
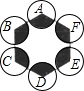如图，正六边形的边长为10，分别以正六边形的顶点A、B、C、D、E、F为圆心，画6个全等的圆．若圆的半径为x，且0＜x≤5，阴影部分的面积为y，能反映y与x之间函数关系的大致图形是（ ）
如图，正六边形的边长为10，分别以正六边形的顶点A、B、C、D、E、F为圆心，画6个全等的圆．若圆的半径为x，且0＜x≤5，阴影部分的面积为y，能反映y与x之间函数关系的大致图形是（ ）| A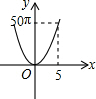． |  | B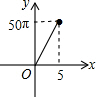． |  | C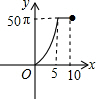． |  | D． |  |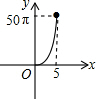
20．2-2的值为（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $-\frac{1}{4}$ |