题目内容
20.2-2的值为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
分析 根据负整数指数幂的运算方法:a-p=$\frac{1}{{a}^{p}}$,求出2-2的值是多少即可.
解答 解:∵2-2=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$,
∴2-2的值为$\frac{1}{4}$.
故选:C.
点评 此题主要考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

练习册系列答案
相关题目
16.若二项式4a2+ma+1是一个含a的完全平方式,则m等于( )
| A. | 4 | B. | 4或-4 | C. | 2 | D. | 2或-2 |
12.某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需化简):
(2)如果销售这批T恤获得的利润用W元表示,求W与x之间的函数关系式;
(3)如果批发商希望销售这批T恤的利润不低于8000元,那么第二个月的降价幅度应在什么范围内?
(1)填表(不需化简):
| 时 间 | 第一个月 | 第二个月 | 清仓时 |
| 单 价(元) | 80 | 40 | |
| 销售量(件) | 200 |
(3)如果批发商希望销售这批T恤的利润不低于8000元,那么第二个月的降价幅度应在什么范围内?
9.下列计算中,正确的是( )
| A. | 2a2+3a2=5a2 | B. | (a-b)2=a2-b2 | C. | a3•a2=a6 | D. | (-2a3)2=8a6 |


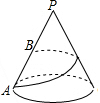 已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)
已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)