题目内容
3．小马虎同学在计算某个多边形的内角和时得到1840°，老师说他算错了，于是小马虎认真地检查了一遍（1）若他检查发现其中一个内角多算了一次，求这个多边形的边数是多少？
（2）若他检查发现漏算了一个内角，求漏算的那个内角是多少度？这个多边形是几边形？
分析 （1）设这个多边形的边数是n，重复计算的内角的度数是x，根据多边形的内角和公式（n-2）•180°可知，多边形的内角度数是180°的倍数，然后利用数的整除性进行求解
（2）设这个多边形的边数是n，没有计算在内的内角的度数是x，根据多边形的内角和公式（n-2）•180°可知，多边形的内角度数是180°的倍数，然后利用数的整除性进行求解．
解答 解：（1）设这个多边形的边数是n，重复计算的内角的度数是x，
则（n-2）•180°=1840°-x，
n=12…40°．
故这个多边形的边数是12．
（2）设这个多边形的边数是n，没有计算在内的内角的度数是x，
则（n-2）•180°=1840°+x，
n=12…40°．
180°-40°=140°，
故漏算的那个内角是140度，这个多边形是十三边形．
点评 本题主要考查了多边形的内角和公式，利用多边形的内角和是180°的倍数是解题的关键．
练习册系列答案
相关题目
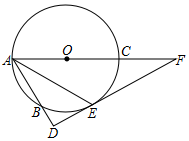如图，AC为⊙O的直径，DAB为⊙O的割线，E为⊙O上一点，弧BE=弧CE，DE⊥AB于D，交AO的延长线于F
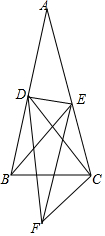在△ABC中，AB=AC，∠A=20°，D、E分别为AB、AC上一点，AD=CD，∠ABE=30°．将CE绕点C逆时针旋转一定角度到F点，使得∠BED=2∠BCF，链接EF和DF，求DE、DF、CD三者的数量关系．
如图，C、D两点将线段AB从左到右依次分成2：3：4三部分，点E、F、G分别是AC、CD、DB的中点，且EG=12cm，则AF=7cm．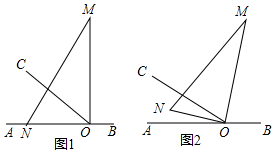
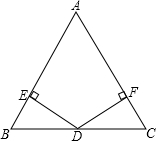【原题再现】课本第81页课内练习第1题：如图，在△ABC中，D为BC边上一点，DB=DC，DE⊥AB于点E，DF⊥AC于点F，且DE=DF，求证：AB=AC．