题目内容
13.如图,已知AB∥CD,分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系,请从你所得两个关系中选出任意一个,说明你探究的结论的正确性.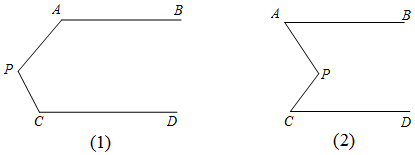
结论:(1)∠APC+∠PAB+∠PCD=360°(2)∠APC=∠PAB+∠PCD
选择结论:∠APC+∠PAB+∠PCD=360°或∠APC=∠PAB+∠PCD,说明理由.
分析 (1)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,同旁内角互补,即可求得∠PAB+∠1=180°,∠2+∠PCD=180°,则可得∠APC+∠PAB+∠PCD=∠PBA+∠1+∠2+∠PCD=360°;
(2)首先过点P作PQ∥AB,又由AB∥CD,可得PQ∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠PAB,∠2=∠PCD,则可得∠APC=∠PAB+∠PCD.
解答 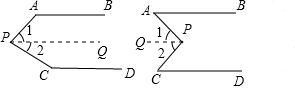 解:(1)∠APC+∠PAB+∠PCD=360°.
解:(1)∠APC+∠PAB+∠PCD=360°.
理由如下:过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠PAB+∠1=180°,∠2+∠PCD=180°,
∵∠APC=∠1+∠2,
∴∠APC+∠PAB+∠PCD=∠PAB+∠1+∠2+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD.
理由如下:过点P作PQ∥AB,
∵AB∥CD,
∴PQ∥AB∥CD,
∴∠1=∠PAB,∠2=∠PCD,
∵∠APC=∠1+∠2=∠PAB+∠PCD,
∴∠APC=∠PAB+∠PCD.
故答案为:∠APC+∠PAB+∠PCD=360°,∠APC=∠PAB+∠PCD;∠APC+∠PAB+∠PCD=360°或∠APC=∠PAB+∠PCD.
点评 此题考查了平行线的性质.注意掌握两直线平行,内错角相等,同位角相等,同旁内角互补与辅助线的添加方法是解此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
18.已知a、b都是不为0的常数,如果多项式(x+a)(x+b)的乘积中不含x项,则有( )
| A. | a-b=0 | B. | ab=1 | C. | a+b=0 | D. | ab=-1 |
5. 如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
 如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )| A. | 5cosα m | B. | $\frac{5}{cosα}$m | C. | 5sinα m | D. | $\frac{5}{sinα}$m |
2. 如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
 如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )| A. | AB | B. | AE | C. | AD | D. | AF |
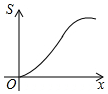
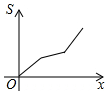
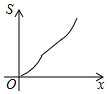
 如图所示,已知等腰梯形ABCD,AD∥BC,若动直线1垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )
如图所示,已知等腰梯形ABCD,AD∥BC,若动直线1垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )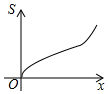
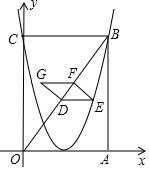 如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造?DEFG,则?DEFG周长的最大值为$\frac{243}{40}$.
如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造?DEFG,则?DEFG周长的最大值为$\frac{243}{40}$.