题目内容
9.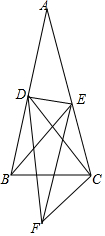 在△ABC中,AB=AC,∠A=20°,D、E分别为AB、AC上一点,AD=CD,∠ABE=30°.将CE绕点C逆时针旋转一定角度到F点,使得∠BED=2∠BCF,链接EF和DF,求DE、DF、CD三者的数量关系.
在△ABC中,AB=AC,∠A=20°,D、E分别为AB、AC上一点,AD=CD,∠ABE=30°.将CE绕点C逆时针旋转一定角度到F点,使得∠BED=2∠BCF,链接EF和DF,求DE、DF、CD三者的数量关系.
分析 如图,作∠BCG=20°,连结GE,把△DEC绕点C逆时针旋转至△MFC处.根据等腰三角形的性质得到∠ABC=∠ACB=80°,推出△CGE是等边三角形,根据等边三角形的性质得到GC=GE,∠EGC=60°,求出∠DGE=40°根据等腰三角形的性质得到∠ACD=∠A=20°,得到∠BCD=60°,求得∠CDE=30°,推出∠ECF=120°,根据等腰三角形的性质得到∠FEC=∠CFE=30°,得到∠EDC=∠EFC,推出点C,E,D,F四点共圆.根据圆周角定理得到∠FDC=∠FEC=30°,∠DEC+∠DFC=180°,根据全等三角形的性质得到DE=MF,∠DEC=∠MFC,∠M=∠CDE=30°,解直角三角形即可得到结论.
解答 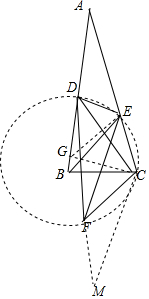 解:如图,作∠BCG=20°,连结GE,把△DEC绕点C逆时针旋转至△MFC处.
解:如图,作∠BCG=20°,连结GE,把△DEC绕点C逆时针旋转至△MFC处.
∵AB=AC,∠A=20°,
∴∠ABC=∠ACB=80°,
∴∠BGC=80°,
∴CB=CG,∠GCE=60°,
∵∠ABE=30°,
∴∠CBE=50°,
∴∠BEC=50°,
∴CB=CE∴CG=CE,
∴△CGE是等边三角形,
∴GC=GE,∠EGC=60°,
∴∠DGE=40°
∵AD=CD,
∴∠ACD=∠A=20°,
∴∠BCD=60°,
∴∠GCD=40°=∠CDG,
∴GC=GD=GE,
∴∠GED=∠GDE=70°,∠GCD=∠GDC=40°,
∴∠CDE=30°,
∴∠DEA=50°,
∴∠DEB=80°,
∵∠BED=2∠BCF,
∴∠BCF=40°,
∴∠ECF=120°,
∵CE=CF,
∴∠FEC=∠CFE=30°,
∴∠EDC=∠EFC,
∴点C,E,D,F四点共圆.
∴∠FDC=∠FEC=30°,∠DEC+∠DFC=180°,
∵△DEC≌△MFC,
∴DE=MF,∠DEC=∠MFC,∠M=∠CDE=30°,
∴∠DFC+∠MFC=180°,
∴D,F,M共线.
在△DMC中,∠M=∠MDC=30°,
∴DM=$\sqrt{3}$DC,
∴DE+DF=$\sqrt{3}$DC.
点评 本题考查了旋转的性质,等腰三角形的性质,四点共圆,圆周角定理,解直角三角形,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{4}$ |
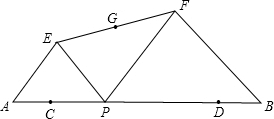 如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )
如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( ) 如图,数轴上点A,B所表示的数分别是4,8.
如图,数轴上点A,B所表示的数分别是4,8.