题目内容
12.一只不透明的袋子中装有白、红、黑三种不同的球,其中白球有3个,红球有8个,黑球有m个,这些球除颜色外完全相同.若从袋子中任意取一个球,摸到黑球的可能性最小,则m的值是1或2.分析 根据摸到哪种球的可能性最小,哪种球的数量最少确定答案即可.
解答 解:∵袋子中装有白、红、黑三种不同的球,其中白球有3个,红球有8个,黑球有m个,摸到黑球的可能性最小,
∴m的值最小,
∴m的值可能为1或2,
故答案为:1或2.
点评 本题考查了可能性的大小的知识,解题的关键是能够根据可能性的大小确定求的数量的多少,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.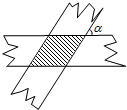 如图,把两条宽度都是1的纸条,其中一条对折后再两条交错地叠在一起,相交成角α,则重叠部分的面积是( )
如图,把两条宽度都是1的纸条,其中一条对折后再两条交错地叠在一起,相交成角α,则重叠部分的面积是( )
 如图,把两条宽度都是1的纸条,其中一条对折后再两条交错地叠在一起,相交成角α,则重叠部分的面积是( )
如图,把两条宽度都是1的纸条,其中一条对折后再两条交错地叠在一起,相交成角α,则重叠部分的面积是( )| A. | 2sinα | B. | 2cosα | C. | $\frac{1}{sinα}$ | D. | $\frac{1}{2cosα}$ |
2. 如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
 如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )
如图,在△ABC中,AD是高,AE是∠BAC的平分线,AF是BC边上的中线,则下列线段中,最短的是( )| A. | AB | B. | AE | C. | AD | D. | AF |
 如图,数轴上点A,B所表示的数分别是4,8.
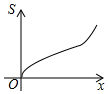
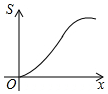
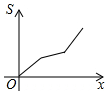
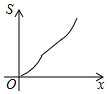
如图,数轴上点A,B所表示的数分别是4,8. 如图所示,已知等腰梯形ABCD,AD∥BC,若动直线1垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )
如图所示,已知等腰梯形ABCD,AD∥BC,若动直线1垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )