题目内容
11.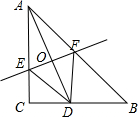 如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F.(1)当CD=$\sqrt{2}$时,求AO的长;
(2)当四边形AEDF是菱形时,求CD的长.
分析 (1)由勾股定理求出AD,得出AO=$\frac{1}{2}$AD=$\frac{\sqrt{6}}{2}$即可;
(2)由等腰直角三角形的性质得出∠B=45°,由菱形的性质得出DE=DF,DE∥AB,DF∥BC,得出∠C=∠FDB=90°,∠EDC=∠B=45°,证出DF=BD=DE,CD=CE,由勾股定理得出方程,解方程即可.
解答 解:(1)∵EF垂直平分AD,
∴AO=DO=$\frac{1}{2}$AD,
∵∠C=90°,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{2})^{2}}$=$\sqrt{6}$,
∴AO=$\frac{1}{2}$AD=$\frac{\sqrt{6}}{2}$;
(2)∵AC=BC,∠C=90°,
∴∠B=45°,
∵四边形AEDF是菱形,
∴DE=DF,DE∥AB,DF∥BC,
∴∠C=∠FDB=90°,∠EDC=∠B=45°,
∴DF=BD=DE,CD=CE,
∵DE2=CD2+CE2,
∴(2-CD)2=2CD2,
∴CD=2$\sqrt{2}$-2.
点评 本题考查了菱形的性质、勾股定理、等腰直角三角形的性质与判定;熟练掌握菱形的性质,由勾股定理得出方程是解决(2)的关键.

练习册系列答案
相关题目
1. 如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
 如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )
如图,A、O、B在一条直线上,∠1+∠2=90°,∠COD=90°,则图中互补的角有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
 已知:如图,已知△ABC.
已知:如图,已知△ABC.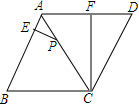 如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.
如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.
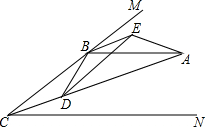 如图,已知CA平分∠MCN,AB∥CN,点D是线段CA上任意点,且BD=BE,∠DBE=∠CBA,连结AE,DE.
如图,已知CA平分∠MCN,AB∥CN,点D是线段CA上任意点,且BD=BE,∠DBE=∠CBA,连结AE,DE. a、b、c三个数在数轴上的位置如图所示,则化简|a-b|-|a-c|的结果是2a-b-c.
a、b、c三个数在数轴上的位置如图所示,则化简|a-b|-|a-c|的结果是2a-b-c.