题目内容
6.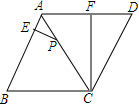 如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.
如图,在菱形ABCD中,点P在对角线AC上,且PC=2PA,PE⊥AB于E,CF⊥AD于F,PE=2,求CF的长.
分析 首先根据菱形的性质可得∠EAP=∠FAC,再有∠AEP=∠AFC=90°可证明△AEP∽△AFC,根据相似三角形的性质可得$\frac{AP}{AC}$=$\frac{EP}{FC}$,然后再根据PC=2PA可得$\frac{AP}{AC}$=$\frac{EP}{FC}$=$\frac{1}{3}$,再把PE=2,可求CF的长.
解答 解:∵四边形ABCD是菱形,
∴∠EAP=∠FAC,
∵PE⊥AB于E,CF⊥AD于F,
∴∠AEP=∠AFC=90°,
∴△AEP∽△AFC,
∴$\frac{AP}{AC}$=$\frac{EP}{FC}$,
∵PC=2PA,
∴$\frac{AP}{AC}$=$\frac{1}{3}$,
∴$\frac{EP}{FC}$=$\frac{1}{3}$,
∵PE=2,
∴CF=6.
点评 此题主要考查了相似三角形的判定和性质,以及菱形的性质,关键是掌握菱形的对角线平分每一组对角.两个角对应相等的两个三角形相似.

练习册系列答案
相关题目
14.单项式2amb1-2n与a3b9的和是单项式,则(m+n)2015=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 0或1 |
1. 如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )
如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )
 如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )
如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )| A. | 20° | B. | 45° | C. | 60° | D. | 40° |
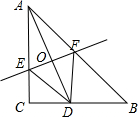 如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F. 如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.
如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.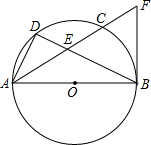 如图,AB是⊙O的直径,点D是弧AC的中点,弦AC与BD相交于点E,DE=3,EB=6.
如图,AB是⊙O的直径,点D是弧AC的中点,弦AC与BD相交于点E,DE=3,EB=6.