题目内容
3.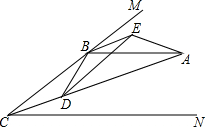 如图,已知CA平分∠MCN,AB∥CN,点D是线段CA上任意点,且BD=BE,∠DBE=∠CBA,连结AE,DE.
如图,已知CA平分∠MCN,AB∥CN,点D是线段CA上任意点,且BD=BE,∠DBE=∠CBA,连结AE,DE.(1)求证:CD=AE;
(2)若BC=13,AC=24.求:
①BD的最小值;②△BDE周长的最小值.
分析 (1)要证CD=AE,可利用角平分线的性质,全等三角形性质,证明△CDB≌△AEB即可证得;
(2)①要求BD的最小值,要运用垂线段定理,等腰三角形的性质,勾股定理,从而求得BD的最小值;
②利用轴对称性质,求出△BDE周长的最小值.
解答 (1)证明:∵AC平分∠MCN,
∴∠ACB=∠ACN,
又∵AB∥CN,
∴∠CAN=∠CAB,
∴∠BCA=∠BAC,
∴CB=AB=13,
又∵∠CBA=∠DBE,
∴∠CBD=∠ABE,
在△CDB和△AEB中,
$\left\{\begin{array}{l}{CB=AB}\\{∠CBD=∠ABE}\\{BD=BE}\end{array}\right.$,
∴△CDB≌△AEB(SAS),
∴CD=AE;
(2)解:①由(1)知CB=AB=13,
当BD⊥AC时,BD最小,
∵BC=AB
∴CD=AD=$\frac{1}{2}$AC=12,
在Rt△BCD中,∠BDC=90°,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=5,
∴BD最小为5;
②BD最小时,周长最小BD=BE=5,
∵∠DBE=∠CBA,AB=BC,BE=BD,即$\frac{AB}{BC}=\frac{DB}{BE}$,
∴△ABC∽△DBE,
∴△ABC与△DBE周长之比=BC:BD,
∴当BD最小时,△DBE周长最小,
△ABC的周长为:13+13+24=50,
∴△DBE的最小周长为50×$\frac{5}{13}=\frac{250}{13}$
点评 本题考查了全等三角形的判定和性质,角平分线的性质,勾股定理,垂线段定理.找出全等三角形的条件,运用等腰三角形的性质,轴对称性质是解决此题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
13.在Rt△ABC中,∠C=90°,若BC=1,AC=2,则cosA的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
14.单项式2amb1-2n与a3b9的和是单项式,则(m+n)2015=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 0或1 |
8.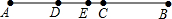 如图,点C为线段AB上一点,CB=a,D、E两点分别为AC、AB的中点,则线段DE的长为( )(用含a的代数式表示)
如图,点C为线段AB上一点,CB=a,D、E两点分别为AC、AB的中点,则线段DE的长为( )(用含a的代数式表示)
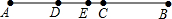 如图,点C为线段AB上一点,CB=a,D、E两点分别为AC、AB的中点,则线段DE的长为( )(用含a的代数式表示)
如图,点C为线段AB上一点,CB=a,D、E两点分别为AC、AB的中点,则线段DE的长为( )(用含a的代数式表示)| A. | $\frac{2}{3}$a | B. | $\frac{1}{4}$a | C. | $\frac{1}{2}$a | D. | $\frac{1}{3}$a |
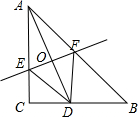 如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F. 如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.
如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.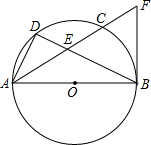 如图,AB是⊙O的直径,点D是弧AC的中点,弦AC与BD相交于点E,DE=3,EB=6.
如图,AB是⊙O的直径,点D是弧AC的中点,弦AC与BD相交于点E,DE=3,EB=6.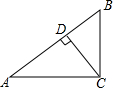 如图,在Rt△ABC中,BC=3,AC=4,CD⊥AB,则CD的长为$\frac{12}{5}$.
如图,在Rt△ABC中,BC=3,AC=4,CD⊥AB,则CD的长为$\frac{12}{5}$.