题目内容
2.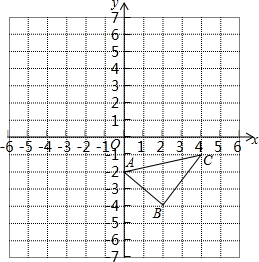 已知:如图,已知△ABC.
已知:如图,已知△ABC.(1)分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2;
(2)求△ABC的面积;
(3)在x轴上画出点P,使△PAB的周长最小.
分析 (1)作出各点关于x、y轴的对称点,再顺次连接即可;
(2)利用矩形的面积减去各顶点上三角形的面积即可;
(3)连接AB1交x轴于点P,则P点即为所求点.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)S△ABC=3×4-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×3
=12-2-2-3
=5;
(3)连接AB1交x轴于点P,则P点即为所求点.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.在Rt△ABC中,∠C=90°,若BC=1,AC=2,则cosA的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
10.某公司今年前三季度实现销售收入约为27.39亿元,那么这个数值精确到( )
| A. | 亿位 | B. | 百分位 | C. | 千万位 | D. | 百万位 |
14.单项式2amb1-2n与a3b9的和是单项式,则(m+n)2015=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 0或1 |
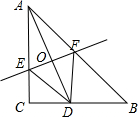 如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,∠C=90°,AC=BC=2,点D在BC上(不与点B,C重合),连接AD,EF为AD的垂直平分线,分别交AC,AD,AB于点E,O,F.