题目内容
11.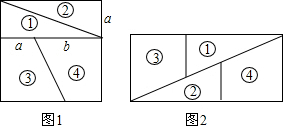 如图,若将如图(1)所示的正方形剪成四块,恰能拼成如图(2)所示的长方形,设a=1,则b的值为( )
如图,若将如图(1)所示的正方形剪成四块,恰能拼成如图(2)所示的长方形,设a=1,则b的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}+3}{2}$ | D. | $\sqrt{2}$+1 |
分析 根据左图可以知道图形是一个正方形,边长为(a+b),右图是一个长方形,长宽分别为(b+a+b)、b,并且它们的面积相等,由此即可列出等式(a+b)2=b(b+a+b),解方程即可求出$\frac{a}{b}$.
解答 解:依题意得(a+b)2=b(b+a+b),
整理得:a2+b2+2ab=2b2+ab
则a2-b2+ab=0,
方程两边同时除以b2,
则($\frac{a}{b}$)2-1+$\frac{a}{b}$=0,
解得:$\frac{a}{b}$=$\frac{-1±\sqrt{5}}{2}$,
∵$\frac{a}{b}$不能为负,
∴$\frac{a}{b}$=$\frac{\sqrt{5}-1}{2}$,
∵a=1,
∴b=$\frac{\sqrt{5}+1}{2}$,
故选B.
点评 此题主要考查了图形的剪拼,此题是一个信息题目,首先正确理解题目的意思,然后会根据题目隐含条件找到数量关系,然后利用数量关系列出方程解决问题.

练习册系列答案
相关题目
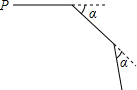 小明从P点出发,沿直线前进10米后向右转a,接着沿直线前进10米,再向右转a,…,照这样走下去,第一次回到出发地点P时,一共走了120米,则a的度数是30°.
小明从P点出发,沿直线前进10米后向右转a,接着沿直线前进10米,再向右转a,…,照这样走下去,第一次回到出发地点P时,一共走了120米,则a的度数是30°. 解不等式(3x+4)(3x-4)-x(x-4)>8(x+1)2,并把它的解集在数轴上表示出来.
解不等式(3x+4)(3x-4)-x(x-4)>8(x+1)2,并把它的解集在数轴上表示出来.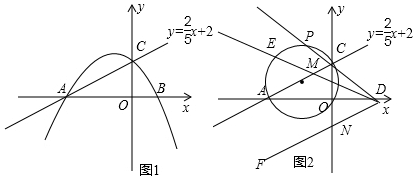
 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴相交于点A,B,若其对称轴为直线x=2,则OB-OA的值为4.
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴相交于点A,B,若其对称轴为直线x=2,则OB-OA的值为4.