题目内容
20．
如图所示，二次函数y=ax2+bx+c（a≠0）的图象与x轴相交于点A，B，若其对称轴为直线x=2，则OB-OA的值为4．
分析 先A（x1，0），B（x2，0），可知x1、x2是方程ax2+bx+c=0的两个根，根据对称轴得：b=-4a，由根与系数的关系可计算OB-OA的值．
解答 解：设A（x1，0），B（x2，0），
则x1、x2是方程ax2+bx+c=0的两个根，
∵抛物线的对称轴是：x=2，
∴-$\frac{b}{2a}$=2，
∴b=-4a，
由图可知：x1＜0，x2＞0，
∴OB-OA=x2-（-x1）=x2+x1=-$\frac{b}{a}$=-$\frac{-4a}{a}$=4，
故答案为：4．
点评 本题考查了二次函数图象对称轴、一元二次方程根与系数的关系，属于基础题，关键是结合图象进行解题．
练习册系列答案
阅读快车系列答案
相关题目
10．在△ABC中，∠A=$\frac{1}{3}$∠B=$\frac{1}{5}$∠C，则△ABC是（ ）
| A． | 钝角三角形 | B． | 直角三角形 | C． | 锐角三角形 | D． | 无法确定 |
11．
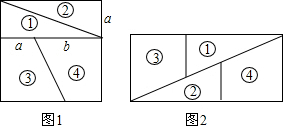如图，若将如图（1）所示的正方形剪成四块，恰能拼成如图（2）所示的长方形，设a=1，则b的值为（ ）
如图，若将如图（1）所示的正方形剪成四块，恰能拼成如图（2）所示的长方形，设a=1，则b的值为（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\frac{\sqrt{5}+3}{2}$ | D． | $\sqrt{2}$+1 |
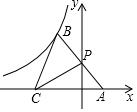如图，双曲线y=$\frac{k}{x}$经过第二象限的点B，点P在y轴上，点A在x轴上，且点B与点A关于点P对称，若OC=2OA，△BCP的面积为4，则k的值是-$\frac{16}{3}$．
5．甲、乙两名运动员每人射击10次，平均成绩为9环，要从中选一位发挥稳定的运动员参加市里比赛，则需关注的统计量是（ ）
| A． | 众数 | B． | 方差 | C． | 中位数 | D． | 平均数 |
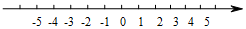在数轴上表示下列各数，并用“＜”连接起来．