题目内容
3.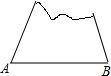 一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
分析 分别过点A和点B作出三角形的两条高线,然后两条高线的交点作AB的垂线,该直线即可AB边上的高所在的直线.
解答 解:如图所示:
①分别过点A、点B作三角形的高线AC、BD,AC与BD相交于点O;
②过点O作OE⊥AB,垂足为E;
③OE即为AB边上的高所在的直线.
理由:∵AC、BD是三角形的高线,锐角三角形的三高线相交于一点,
∴点O在AB边的上高线上.
∵过点O有且只有一条直线与AB垂直,
∴OE为AB边上的高所在的直线.
点评 本题主要考查的是作图-应用与设计作图,明确三角形的三条高线所在的直线相交于一点是解题的关键.

练习册系列答案
相关题目
14. 有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
 有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )
有理数a,b在数轴上的位置如图所示,则下列各式成立的是( )| A. | a>-b | B. | -b>0 | C. | b-a>0 | D. | -ab<0 |
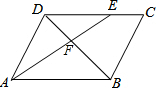 如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
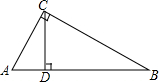 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值. 如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.
如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.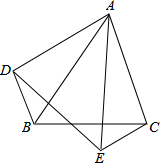 如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC.
如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE,求证:BD=EC.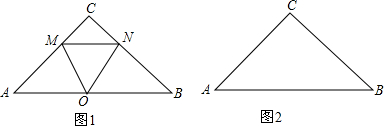
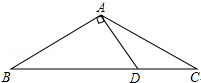 如图,△ABC中,AB=AC,∠CAD=30°,AB⊥AD,AD=4,求BC的长.
如图,△ABC中,AB=AC,∠CAD=30°,AB⊥AD,AD=4,求BC的长.