题目内容
13.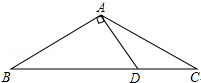 如图,△ABC中,AB=AC,∠CAD=30°,AB⊥AD,AD=4,求BC的长.
如图,△ABC中,AB=AC,∠CAD=30°,AB⊥AD,AD=4,求BC的长.
分析 根据垂直的定义得到∠BAC=120°,根据等腰三角形的性质得到∠B=∠C=30,根据直角三角形的性质求出BD=2AD,根据等腰三角形的性质得到CD=AD,结合图形计算即可.
解答 解:∵∠CAD=30°,AB⊥AD,
∴∠BAC=120°,
∵AB=AC,
∴∠B=∠C=30,
∴BD=2AD=8,
∵∠CAD=∠C=30°,
∴CD=AD=4,
∴BC=BD+CD=8+4=12.
点评 本题考查的是直角三角形的性质和等腰三角形的性质,掌握在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
1.已知(m-n)2=32,(m+n)2=4000,则m2+n2的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 4032 |
5.如果2x与x-3的值互为相反数,那么x等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
2.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”,应先假设( )
| A. | 两个锐角都小于45° | B. | 两个锐角都大于45° | ||
| C. | 一个锐角小于45° | D. | 一个锐角小于或等于45° |
3.在Rt△ABC中,∠C为直角,AC=5,AB=13,则下列正确的是( )
| A. | sinA=$\frac{5}{13}$ | B. | cotA=$\frac{13}{5}$ | C. | tanA=$\frac{12}{5}$ | D. | cosA=$\frac{12}{13}$ |
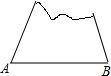 一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.