题目内容
9.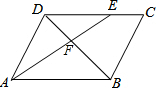 如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
分析 根据平行四边形的性质得到AB∥CD,CD=AB=6,由平行线的性质得到∠AED=∠EAB,由角平分线的定义得到∠DAE=∠BAE,等量代换得到∠DAE=∠AED,根据等腰三角形的判定得到DE=AD=4,由相似三角形的性质得到$\frac{DF}{BF}=\frac{DE}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$,
解答 解:在?ABCD中,
∵AB∥CD,CD=AB=6,
∴∠AED=∠EAB,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠DAE=∠AED,
∴DE=AD=4,
∵DE∥AB,
∴△DEF∽△ABF,
∴$\frac{DF}{BF}=\frac{DE}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,角平分线的定义,熟练掌握相似三角形的判定是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知一元二次方程2x2+x+k=0无实数根,那么反比例函数y=$\frac{k}{x}$的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 无法确定 |
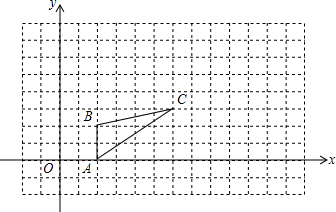 如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).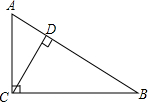 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.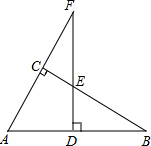 如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.
如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.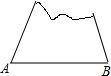 一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.
一个缺角的三角形残片如图所示,不恢复这个残角,你能否作出AB边上的高所在的直线?试说明理由.