题目内容
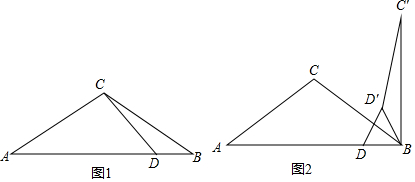
14.如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,BD的长为一元二次方程x2-2x=6-3x的根,cos∠ADC=$\frac{\sqrt{2}}{2}$.(1)求BD的长;
(2)求AB的长;
(3)将图1中的△BCD绕点B顺时针旋转α(0°<α≤360°)得到△BC′D′,连接DD′,如图2所示,当△DBD′与△ACB相似时,直接写出α的度数.
分析 (1)解方程即可解决问题.
(2)如图1中,过点C作CH⊥AB于H.在Rt△CHD中,由cos∠ADC=$\frac{\sqrt{2}}{2}$,推出∠ADC=45°,设CH=x,则DH=x,由DB=2,可得BH=x+2,在Rt△CHA中,∠A=30°,可得AH=CH÷tan30°=$\sqrt{3}$x,因为AC=BC,所以BH=AH=$\frac{1}{2}$AB,可得方程$\sqrt{3}$x=x+2,解方程即可解决问题.
(3)画出图形即可解决问题.
解答 解:(1)解方程x2-2x=6-3x的得到x=2或-3,
∵线段的长度为正,
∴BD=2.
(2)如图1中,过点C作CH⊥AB于H.
在Rt△CHD中,∵cos∠ADC=$\frac{\sqrt{2}}{2}$,
∴∠ADC=45°,设CH=x,则DH=x,
∵DB=2,
∴BH=x+2,
在Rt△CHA中,∠A=30°,
∴AH=CH÷tan30°=$\sqrt{3}$x,
∵AC=BC,
∴BH=AH=$\frac{1}{2}$AB,
∴$\sqrt{3}$x=x+2,
∴x=$\sqrt{3}$+1,
∴BH=$\sqrt{3}$+3,
∴AB=2($\sqrt{3}$+3)
(3)如图2,3中,

当α的度数为120°或240°时,易知∠BDD′=∠BD′D=∠A=∠ABC=30°,
∴△DBD′∽△ACB.
∴α的度数为120°或240°.
点评 本题考查相似形综合题、锐角三角函数、勾股定理、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,考虑问题要全面,属于中考压轴题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
2.在△ABC中,∠A:∠B:∠C=3:4:5,则∠C等于( )
| A. | 75° | B. | 60° | C. | 45° | D. | 90° |
19.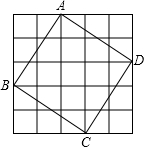 如图,在5×5的方格中,有一个正方形ABCD,假设每一个小方格的边长为1个单位长度,则正方形的边长为( )
如图,在5×5的方格中,有一个正方形ABCD,假设每一个小方格的边长为1个单位长度,则正方形的边长为( )
 如图,在5×5的方格中,有一个正方形ABCD,假设每一个小方格的边长为1个单位长度,则正方形的边长为( )
如图,在5×5的方格中,有一个正方形ABCD,假设每一个小方格的边长为1个单位长度,则正方形的边长为( )| A. | $\sqrt{12}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | $\sqrt{15}$ |
6.已知函数y=x2-2mx+2016(m为常数)的图象上有三点:A(x1,y1),B(x2,y2),C(x3,y3),其中x1=-$\sqrt{2}$+m,x2=$\frac{2}{3}$+m,x3=m-1,则y1、y2、y3的大小关系是( )
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y1<y2<y3 | D. | y2<y3<y1 |
4.边长分别为5、5、6的三角形的内切圆的半径为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
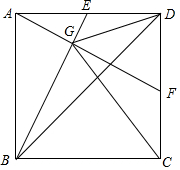 正方形ABCD中,E、F分别是AD、DC的中点,BE和AF交于点G,∠DGF=∠DBC,求证:GC=BC.
正方形ABCD中,E、F分别是AD、DC的中点,BE和AF交于点G,∠DGF=∠DBC,求证:GC=BC.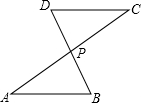 如图,AC与BD交于点P,AP=CP,从以下四个论断①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是③.
如图,AC与BD交于点P,AP=CP,从以下四个论断①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是③.