题目内容
3.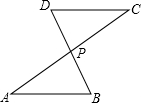 如图,AC与BD交于点P,AP=CP,从以下四个论断①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是③.
如图,AC与BD交于点P,AP=CP,从以下四个论断①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是③.
分析 ①当添加∠B=∠D后可根据全等三角形的判定定理AAS证出△ABD≌△CDB,①可以;②当添加BP=DP后可根据全等三角形的判定定理SAS证出△ABD≌△CDB,②可以;③当添加AB=CD后,利用SSA不能证出△ABD≌△CDB,③不可以;④根据AB∥CD即可找出∠B=∠C,再根据全等三角形的判定定理ASA即可证出△ABD≌△CDB,④可以.综上即可得出结论.
解答 解:①在△ABD和△CDB中,$\left\{\begin{array}{l}{∠B=∠D}\\{∠APB=∠CPD}\\{AP=CP}\end{array}\right.$,
∴△ABD≌△CDB(AAS);
②在△ABD和△CDB中,$\left\{\begin{array}{l}{AP=CP}\\{∠APB=∠CPD}\\{BP=DP}\end{array}\right.$,
∴△ABD≌△CDB(SAS);
③∵在△ABD和△CDB中,AP=CP、∠APB=∠CPD、AB=CD不满足全等三角形的判定定理的条件,
∴添上AB=CD不能证出△APB≌△CPD;
④∵AB∥CD,
∴∠A=∠C.
在△ABD和△CDB中,$\left\{\begin{array}{l}{∠A=∠C}\\{AP=CP}\\{∠APB=∠CPD}\end{array}\right.$,
∴△ABD≌△CDB(ASA).
故答案为:③.
点评 本题考查了全等三角形的判定,熟练掌握各全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
8.有下列事件,其中是必然事件的有( )
①367人中必有2人的生日相同;
②在标准大气压下,温度低于0℃时冰融化;
③抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;
④如果a、b为实数,那么a+b=b+a.
①367人中必有2人的生日相同;
②在标准大气压下,温度低于0℃时冰融化;
③抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;
④如果a、b为实数,那么a+b=b+a.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.比-4小2的数是( )
| A. | -1 | B. | -2 | C. | -6 | D. | 0 |
13.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6m3时时,水费按每立方米a元收费,超过6m3时,超过的部分每立方米按c元收费,不超过的部分每立方米仍按a元收费该市某户今年9、10月份的用水量和所交水费如下表所示:
设某户每月用水量x(立方米),应交水费y(元)
(1)a=1.5,c=6;
(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;
(3)若该户11月份用水8m3,则该户应交水费多少元?
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
(1)a=1.5,c=6;
(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;
(3)若该户11月份用水8m3,则该户应交水费多少元?
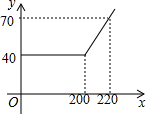 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.