题目内容
4.边长分别为5、5、6的三角形的内切圆的半径为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
分析 由⊙O是△ABC的内切圆,⊙O切AB于E,切BC于D,根据切线长定理得到BD=BE,求得BD,AD,BE,AE,由勾股定理列方程求解.
解答 解:如图∵⊙O是△ABC的内切圆,
⊙O切AB于E,切BC于D,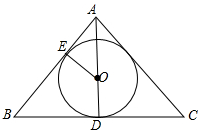
∵AB=AC=5,
∴A,O,D三点共线,
∴BD=$\frac{1}{2}$BC=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4,
∴BE=BD=3,
∴AE=2,
设三角形内切圆的半径为r,
∴(4-r)2=22+r2,
∴r=$\frac{3}{2}$cm,
∴三角形内切圆的半径为$\frac{3}{2}$.
故选:B.
点评 本题主要考查对三角形的内切圆与内心,切线长定理,切线的性质,正方形的性质和判定,勾股定理等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.比-4小2的数是( )
| A. | -1 | B. | -2 | C. | -6 | D. | 0 |
16.$\sqrt{8}$的相反数是( )
| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
13.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6m3时时,水费按每立方米a元收费,超过6m3时,超过的部分每立方米按c元收费,不超过的部分每立方米仍按a元收费该市某户今年9、10月份的用水量和所交水费如下表所示:
设某户每月用水量x(立方米),应交水费y(元)
(1)a=1.5,c=6;
(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;
(3)若该户11月份用水8m3,则该户应交水费多少元?
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
(1)a=1.5,c=6;
(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;
(3)若该户11月份用水8m3,则该户应交水费多少元?