题目内容
20.解方程:(1)125(x-2)3=-343;
(2)2(2x+1)2=4.
分析 (1)负数的立方根是负数,直接开立方即可;
(2)直接开平方计算即可.
解答 解:(1)∵125(x-2)3=-343,
∴(x-2)3=-$\frac{{7}^{3}}{{5}^{3}}$,
∴x-2=-$\frac{7}{5}$,
x=$\frac{3}{5}$;
(2)∵2(2x+1)2=4,
∴(2x+1)2=2,
∴2x+1=$±\sqrt{2}$,
∴x1=$\frac{-1-\sqrt{2}}{2}$,x2=$\frac{-1+\sqrt{2}}{2}$.
点评 本题考查(1)立方根定义:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a的立方根.记作:a3.
(2)正数的立方根是正数,0的立方根是0,负数的立方根是负数.即任意数都有立方根.
(3)求一个数a的立方根的运算叫开立方,其中a叫做被开方数.
平方根的定义:如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.
一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
求一个数a的平方根的运算,叫做开平方.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
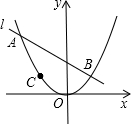 如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.
如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.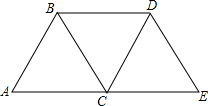 如图,把△ABC按AC方向平移,平移的距离是AC的长度,则平移后点B平移到点D,连接BD后,得到的四边形ACDB和CEDB都是平行四边形吗?
如图,把△ABC按AC方向平移,平移的距离是AC的长度,则平移后点B平移到点D,连接BD后,得到的四边形ACDB和CEDB都是平行四边形吗?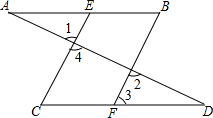 如图,已知AD与AB,CD相交于A,D两点,EC,BF与AB,CD相交于点E,C,B,F,且∠1=∠2,∠B=∠C,
如图,已知AD与AB,CD相交于A,D两点,EC,BF与AB,CD相交于点E,C,B,F,且∠1=∠2,∠B=∠C,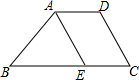 如图,梯形ABCD的上底AD=3,下底BC=8,腰CD=4,求另一腰AB的取值范围.
如图,梯形ABCD的上底AD=3,下底BC=8,腰CD=4,求另一腰AB的取值范围.