题目内容
12.一次函数y=$\frac{1}{2}$x-1的图象分别交x轴,y轴于点A,B,设点P是第四象限内一点,当以点P,A,B为顶点的三角形与△OAB全等时,点P的坐标为($\frac{8}{5}$,-$\frac{16}{5}$)或(2,-1).分析 根据直线方程求得A、B的坐标.需要分类讨论:△PAB≌△OAB、△PBA≌△OAB.
解答 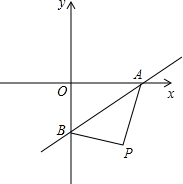 解:∵y=$\frac{1}{2}$x-1,
解:∵y=$\frac{1}{2}$x-1,
∴当x=0时,y=-1.当y=0时,x=2,
∴A(2,0),B(0,-1).
设P(a,b).
①当△PAB≌△OAB时,PA=OA=2,PB=OB=1,
则$\left\{\begin{array}{l}{(x-2)^{2}+{y}^{2}=4}\\{{x}^{2}+(y+1)^{2}=1}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=0}\end{array}\right.$(舍去),$\left\{\begin{array}{l}{x=\frac{4}{5}}\\{y=-\frac{8}{5}}\end{array}\right.$,
即P($\frac{4}{5}$,-$\frac{8}{5}$).
②当△PBA≌△OAB时,PB=OA,PA=OB,则四边形OAPB是矩形,易求P(2,-1);
综上所述,点P的坐标为($\frac{4}{5}$,-$\frac{8}{5}$)或(2,-1).
故答案是:($\frac{4}{5}$,-$\frac{8}{5}$)或(2,-1).
点评 本题考查了全等三角形的判定和一次函数图象上点的坐标特征.推知以点P,A,B为顶点的三角形与△OAB全等时,要分类讨论,以防漏解.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
3.下列各组数中既是方程x-2y=4,又是方程2x+2y=1的解的是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=-\frac{7}{6}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=\frac{3}{2}}\end{array}\right.$ |
17.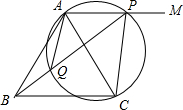 如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
 如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |