题目内容
11.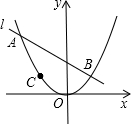 如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.
如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.(1)请直线写出点A坐标及a的值;
(2)当直线l过点B时,求k的值;
(3)在y轴上一点P到A,C的距离和最小,求P点坐标;
(4)在(2)的条件下,x取-2<x<1值时,ax2<kx+2k+2.
分析 (1)把直线解析式整理成关于k的形式,然后令k的系数等于0求解即可得到定点A的坐标,将点A的坐标代入抛物线求解即可得到a的值;
(2)将点B的坐标代入抛物线求解得到b的值,再把点B的坐标代入直线计算即可求出k;
(3)判断出B、C关于y轴对称,再根据轴对称确定最短路线问题,直线AB与y轴的交点即为所求的点P,然后根据直线解析式求解即可;
(4)根据函数图象写出直线在抛物线上方部分的x的取值范围即可.
解答 解:(1)y=kx+2k+2=k(x+2)+2,
当x+2=0,即x=-2时,直线经过定点,
此时,y=2,
所以,A(-2,2),
将点A代入a•(-2)2=2,
解得a=$\frac{1}{2}$;
(2)抛物线解析式为y=$\frac{1}{2}$x2,
x=1时,b=$\frac{1}{2}$×12=$\frac{1}{2}$,
所以,点B(1,$\frac{1}{2}$),
将点B代入直线得,k+2k+2=$\frac{1}{2}$,
解得,k=-$\frac{1}{2}$;
(3)抛物线y=$\frac{1}{2}$x2的对称轴为y轴,
y=当x=-1时,c=$\frac{1}{2}$×(-1)2=$\frac{1}{2}$,
所以,点C(-1,$\frac{1}{2}$),
所以,点B、C关于y轴对称,
由轴对称确定最短路线问题,直线AB与y轴的交点即为所求的点P,
由(2)知,直线AB的解析式为y=-$\frac{1}{2}$x+1,
令x=0,则y=1,
所以,点P的坐标为(0,1);
(4)由图可知,-2<x<1时,ax2<kx+2k+2.
故答案为:-2<x<1.
点评 本题是二次函数综合题型,主要利用了直线过定点的求法,二次函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数的对称性,轴对称确定最短路线问题,二次函数与不等式,难点在于(1)整理成关于k的形式,(3)确定出点P的位置.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 由若干个小正方体摆成的几何体的主视图和左视图如图所示,则小正方体的个数最少是( )
由若干个小正方体摆成的几何体的主视图和左视图如图所示,则小正方体的个数最少是( )| A. | 6 | B. | 9 | C. | 12 | D. | 15 |
| A. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=-\frac{7}{6}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=\frac{3}{2}}\end{array}\right.$ |

 如图,这是某个小区内的道路示意图,小明家住在该小区的A处,他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走,有的道路可以不走)
如图,这是某个小区内的道路示意图,小明家住在该小区的A处,他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走,有的道路可以不走)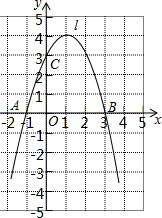 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.