题目内容
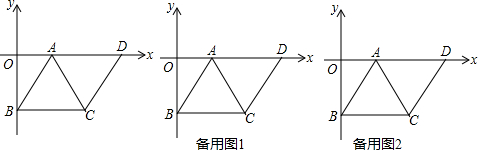
9．
如图，梯形ABCD的上底AD=3，下底BC=8，腰CD=4，求另一腰AB的取值范围．
分析 先证明四边形AECD是平行四边形，得出CE=AD=3，AE=CD=4，求出BE=BC-CE=5，在△ABE中，由三角形的三边关系即可得出结果．
解答 解：∵AD∥BC，AE∥CD，
∴四边形AECD是平行四边形，
∴CE=AD=3，AE=CD=4，
∴BE=BC-CE=5，
在△ABE中，AB的取值范围是5-4＜AB＜5+4，
即1＜AB＜9．
点评 本题考查了梯形的性质、平行四边形的判定与性质以及三角形三边关系；通过证明平行四边形得出对应边相等是解决问题的关键．
练习册系列答案
相关题目
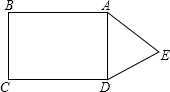如图，这是某个小区内的道路示意图，小明家住在该小区的A处，他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家（每条道路不能重复走，有的道路可以不走）
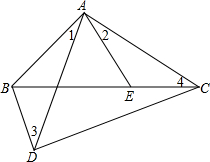如图，D是△ABC外一点，E是边BC上一点，∠1=∠2，∠3=∠4．图中有几对相似的三角形？（不准添加新的字母）请说明理由．