题目内容
 如图,⊙O的直径AB与弦CD互相垂直,垂足为点E,BF∥CD,BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=
如图,⊙O的直径AB与弦CD互相垂直,垂足为点E,BF∥CD,BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=| 3 |
| 4 |
(1)求证:BF是⊙O的切线;
(2)求⊙O的半径;
(3)求弦CD的长.
考点:切线的判定,勾股定理,解直角三角形
专题:证明题
分析:(1)由于直径AB与弦CD互相垂直,BF∥CD,根据平行线的性质得AB⊥BF,于是根据切线的判定定理得到BF是⊙O的切线;
(2)连结BD,如图,根据圆周角定理得∠BCD=∠A,则cosA=cos∠BCD=
,再由AB为直径得到∠ADB=90°,在Rt△ABD中利用余弦的定义可计算出AB=4,从而得到⊙O的半径为2;
(3)连结OD,如图,先在Rt△AED中利用余弦的定义可计算出AE=
,则OE=AE-OA=
,再在Rt△ODE中利用勾股定理计算出DE=
,然后根据垂径定理得到CD=2DE=
.
(2)连结BD,如图,根据圆周角定理得∠BCD=∠A,则cosA=cos∠BCD=
| 3 |
| 4 |
(3)连结OD,如图,先在Rt△AED中利用余弦的定义可计算出AE=
| 9 |
| 4 |
| 1 |
| 4 |
3
| ||
| 4 |
3
| ||
| 2 |
解答: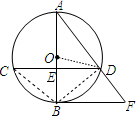 (1)证明:∵直径AB与弦CD互相垂直,BF∥CD,
(1)证明:∵直径AB与弦CD互相垂直,BF∥CD,
∴AB⊥BF,
∴BF是⊙O的切线;
(2)解:连结BD,如图,
∵∠BCD=∠A,
∴cosA=cos∠BCD=
,
∵AB为直径,
∴∠ADB=90°,
在Rt△ABD中,∵cosA=
=
,
∴AB=
=4,
∴⊙O的半径为2;
(3)解:连结OD,如图,
在Rt△AED中,∵cos∠A=
=
,
∴AE=
×3=
,
∴OE=AE-OA=
-2=
,
在Rt△ODE中,∵OD=2,OE=
,
∴DE=
=
,
∵AB⊥CD,
∴CE=DE,
∴CD=2DE=
.
 (1)证明:∵直径AB与弦CD互相垂直,BF∥CD,
(1)证明:∵直径AB与弦CD互相垂直,BF∥CD,∴AB⊥BF,
∴BF是⊙O的切线;
(2)解:连结BD,如图,
∵∠BCD=∠A,
∴cosA=cos∠BCD=
| 3 |
| 4 |
∵AB为直径,
∴∠ADB=90°,
在Rt△ABD中,∵cosA=
| AD |
| AB |
| 3 |
| 4 |
∴AB=
| 3 | ||
|
∴⊙O的半径为2;
(3)解:连结OD,如图,
在Rt△AED中,∵cos∠A=
| AE |
| AD |
| 3 |
| 4 |
∴AE=
| 3 |
| 4 |
| 9 |
| 4 |
∴OE=AE-OA=
| 9 |
| 4 |
| 1 |
| 4 |
在Rt△ODE中,∵OD=2,OE=
| 1 |
| 4 |
∴DE=
| OD2-OE2 |
3
| ||
| 4 |
∵AB⊥CD,
∴CE=DE,
∴CD=2DE=
3
| ||
| 2 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理、垂径定理和解直角三角形.

练习册系列答案
相关题目
对于任何整数m,多项式(4m+5)2-9都能( )
| A、被8整除 |
| B、被m整除 |
| C、被(m-1)整除 |
| D、被(2m-1)整除 |
 如图,AB=DE,AB∥DE,BE=CF.求证:AC=DF.
如图,AB=DE,AB∥DE,BE=CF.求证:AC=DF. 如图,它可以看作“
如图,它可以看作“ ”通过连续平移
”通过连续平移 ”绕中心旋转
”绕中心旋转 如图所示,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c,已知b=2
如图所示,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别是a,b,c,已知b=2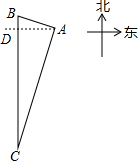 如图,某国3艘炮艇正追袭5条中国渔船,“中国渔政310”船(用“A”表示)接到陆地指挥中心(用“B”表示)命令疾速驰救中国渔船,渔船(用“C”表示)位于陆地指挥中心正南方向.经测定AB=
如图,某国3艘炮艇正追袭5条中国渔船,“中国渔政310”船(用“A”表示)接到陆地指挥中心(用“B”表示)命令疾速驰救中国渔船,渔船(用“C”表示)位于陆地指挥中心正南方向.经测定AB= 如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,AD:DB=1:2,S△ADE=1,则S四边形BCED的值为
如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,AD:DB=1:2,S△ADE=1,则S四边形BCED的值为