题目内容
对于任何整数m，多项式（4m+5）2-9都能（ ）
| A、被8整除 |
| B、被m整除 |
| C、被（m-1）整除 |
| D、被（2m-1）整除 |
考点：因式分解-运用公式法
专题：
分析：将该多项式分解因式，其必能被它的因式整除．
解答：解：（4m+5）2-9
=（4m+5）2-32，
=（4m+8）（4m+2），
=8（m+2）（2m+1），
∵m是整数，而（m+2）和（2m+1）都是随着m的变化而变化的数，
∴该多项式肯定能被8整除．
故选A．
=（4m+5）2-32，
=（4m+8）（4m+2），
=8（m+2）（2m+1），
∵m是整数，而（m+2）和（2m+1）都是随着m的变化而变化的数，
∴该多项式肯定能被8整除．
故选A．
点评：本题考查了因式分解的应用，正确分解因式是解题关键．
练习册系列答案
相关题目
如图，E，F是四边形ABCD的对角线AC上两点，AF=CE，DF=BE，DF∥BE．求证：AB=CD．
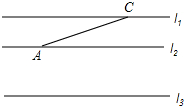如图，已知直线l1∥l2∥l3，且l1，l2之间的距离为1，l2，l3之间的距离为2，点A、C分别在直线l2，l1上，
在四边形ABCD中，AB∥CD，AD∥BC，点E是线段BC的中点，F点在边DC上，AE平分∠BAF．
如图，⊙O的直径AB与弦CD互相垂直，垂足为点E，BF∥CD，BF与弦AD的延长线相交于点F，且AD=3，cos∠BCD=